Comment démontrer que deux droites sont parallèles

Voici un problème de niveau 2

Lire le texte attentivement .
Représenter la situation par un dessin .
A B
(d)
En regardant le dessin, tenter de répondre
à la question .
Le but de la démonstration est à cet instant
fixé . BUT : (d) // (AB)
Sortir une à une les informations
contenues dans le texte .
INFORMATIONS
La phase de préparation
est maintenant achevée
La phase suivante est la
démonstration
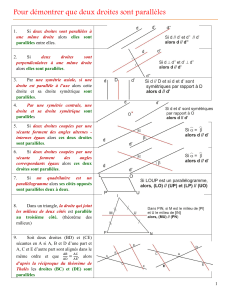
Soit un parallèlogramme ABCD .et une droite (d) parallèle à
la droite (DC) .
Que peut-on dire des droites (d) et (AB) ?
CD
Problème niveau 2
ABCD est un parallèlogramme
(d) // (DC)

A B
(d)
CD
BUT : (d) // (AB)
INFORMATIONS
ABCD est un parallèlogramme
(d) // (DC)
Conclusion
Théorème
Informations
Conclusion
Théorème
Informations
Problème de
niveau 2 .
Donc
Deux blocs
logiques
Par où commence-
t-on ?
Par la fin….
Bien sûr !!!!
(d) // (AB)

A B
(d)
CD
BUT : (d) // (AB)
INFORMATIONS
ABCD est un parallèlogramme
(d) // (DC)
Fiche :Comment démontrer qu’un triangle est isocèle
Fiche :Comment démontrer que deux distances sont
égales
Fiche :Comment démontrer que deux droites sont
perpendiculaires
Fiche :Comment démontrer qu’un quadrilatère est un
rectangle
Fiche :Comment démontrer que deux droites sont
parallèles
Fiche :Comment démontrer que deux distances sont
égales
Fiche :Comment démontrer qu’un triangle est rectangle
Dans quelle fiche se
trouve le théorème
dont on a besoin ?
C’est bien cette
fiche .
Bien observer la
construction pour
choisir le théorème On ne prend pas toujours le
bon du premier coup !!

A B
(d)
CD
BUT : (d) // (AB)
INFORMATIONS
ABCD est un parallèlogramme
(d) // (DC)
Comment démontrer que deux droites
sont parallèles
Si deux droites sont symétriques par rapport à
un point alors elles sont parallèles .
Si deux droites déterminent avec une sécante
des angles alternes-internes de même mesure alors
elles sont parallèles
Si deux droites déterminent avec une sécante
des angles alternes-externes de même mesure alors
elles sont parallèles
Si deux droites déterminent avec une sécante
des angles correspondants de même mesure alors
elles sont parallèles
Si un quadrilatère est un trapèze alors ses
bases sont parallèles
Si un quadrilatère est un parallélogramme
alors ses côtés opposés sont parallèles
Si deux droites sont parallèles à une même
droite alors elles sont parallèles
Si deux droites sont perpendiculaires à une
même droite alors elles sont parallèles
Alors, lequel
choisir ?