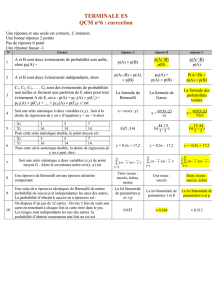
PUC-SP

Émergence du calcul des
probabilités (II)
De l’espérance pascalienne
à la théorie laplacienne

3 - Fondateurs et développeurs
Jacques Bernoulli : l’approche fréquentiste
Abraham de Moivre : la doctrine des chances
Georges Louis Leclerc, comte de Buffon :
probabilités géométriques
Jean Le Rond D’Alembert : probabilités,
mathématiques et réalité ?
Marie-Jean Antoine Caritat, marquis de
Condorcet : didactique et vulgarisation

Jacques Bernoulli
(1654-1705)
Ars Conjectandi, 1713
Jean Bernoulli
1667-1748 Daniel Bernoulli
1700-1782

La famille Bernoulli

Jacques Bernoulli déterministe:
“Tout ce qui bénéficie sous le soleil de l'être ou du devenir,
passé, présent ou futur, possède toujours en soi et objectivement
une certitude totale.
C'est évident du présent et du passé,ce qui est ou a éténe peut
pas ne pas être ou avoir été.
Sur le futur il n'y a pas àdiscuter ; cependant ce n'est pas par la
nécessitéde quelque destin qu'il ne peut pas ne pas advenir, mais
en raison soit de la prescience soit de la prédétermination divine ;
car si n’arrivait pas avec certitude tout ce qui est futur, on ne voit
pas comment le Créateur suprême pourrait conserver entière la
gloire de son omniscience et de son omnipotence.
Quant àdire comment cette certitude de l'avenir peut subsister
avec la contingence ou la libertédes causes secondes, que d'autres
en disputent ; pour nous, nous ne voulons pas toucher aux points
étrangers au but que nous visons. ”
Ars Conjectandi, quatrième partie, chapitre I