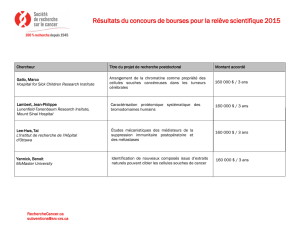
Règle de l`Hospital

Règle de L’Hospital
Comment régler presque tous les cas
d’indétermination dans le calcul des limites ?

Un peu d’histoire …
Guillaume de L'Hospital, marquis de Saint Mesme, est un élève de Jean
Bernoulli qui lui apprend le calcul différentiel. C'est ainsi que L'Hospital est le
premier à écrire un traité sur ce nouvel outil, le livre Analyse des infiniment
petits pour l'intelligence des lignes courbes (1696). C'est dans ce livre
qu'apparait la célèbre règle de L'Hospital, qui permet parfois de lever des
formes indéterminées du type 0/0. En 1707, L'Hospital publie également un
traité sur les coniques (Traité analytique des sections coniques), qui sera
pendant un siècle un classique du genre.
La connaissance du calcul différentiel fait que L'Hospital est un de ceux qui a
résolu le problème de la brachistochrone, indépendamment de mathématiciens
prestigieux comme Newton ou Leibniz. Toutefois, ce mérite est entaché par les
déclarations, après la mort de son élève, de Jean Bernoulli : à la suite d'un
arrangement financier, L'Hospital aurait publié sous son propre nom des
résultats dus à Bernoulli.
Notez que l’Hospital est de la même époque que Newton et Leibniz.

Règle de l’Hospital
Soit fet gdeux fonctions continues sur un
intervalle [c,d] telles que:
1. lim ( ) 0 et lim ( ) 0 où ] , [
x a x a
f x g x a c d
2. '( ) et '( ) sont continues enf x g x x a
3. '( ) 0 ] , [ { }\g x x c d a  
si cette limite existe ou est infinie
( ) '( )
lim lim
( ) '( )
x a x a
f x f x
g x g x
Alors

Preuve
Puisque fet gsont continues, on a par l’hypothèse 1 que f(a) = g(a) = 0.
( ) ( ) ( )
lim lim
( ) ( ) ( )
x a x a
f x f x f a
g x g x g a
Donc
( ) ( )
lim ( ) ( )
xa
f x f a
xa
g x g a
xa
( ) ( )
lim
( ) ( )
lim
xa
xa
f x f a
xa
g x g a
xa
'( )
'( )
fa
ga
lim '( )
lim '( )
xa
xa
fx
gx
'( )
lim '( )
xa
fx
gx
car fet g sont dérivables en x = a
car f’et g’ sont continues en x = a
C.Q.F.D.

Autres indéterminations
Forme indéterminée Étapes à suivre
Utiliser directement la règle de l’Hospital
1. Transformer le produit f(x) g(x ) sous la forme
pour se ramener au cas précédent
2. Utiliser la règle de l’Hospital
1. Utiliser des manipulations algébriques (identités
trigonométriques, dénominateur commun, conjugué…)
pour se ramener à la forme de base (0/0ou /)
2. Utiliser la règle de l’Hospital
1. Poser yégal à la fonction dans la limite
2. Prendre le log naturel de chaque membre de l’égalité
3. Utiliser la propriété ln(Ak) = kln(A), puis prendre la
limite
4. Évaluer la limite de forme 0() obtenue
5. Revenir à la limite initiale en prenant l’exponentielle
0ou
0
0 ( ) 
00
0 ou ou 1
( ) ( )
ou
11
( ) ( )
f x g x
g x f x