Chapitre 7 Calcul de primitive

Chapitre 7
Calcul de primitive
49

50 CHAPITRE 7. CALCUL DE PRIMITIVE
7.1 Th´eorie
7.1.1 Primitives et int´egrales
D´efinition : Soit fune fonction d´efinie sur un intervalle I. On dit que F
est une primitive de fsur Isi Fest d´erivable sur Iet F�=f.
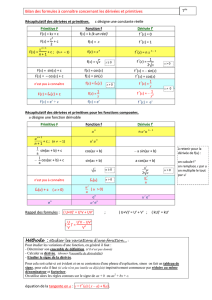
Exemples : La fonction ln est une primitive de la fonction inverse sur
]0; +∞[, la fonction exp est une primitive d’elle-mˆeme sur R,lafonction
sin est une primitive de la fonction cos, la fonction f1:x→ 3
4x4+5x2+18
est une primitive de la fonction f2:x→ 3x3+10xsur R,mais´egalement
f1−12 ou encore f1+5421 (puisque les constantes disparaissent `a la d´eriva-
tion).
On voit sur le dernier exemple qu’une fonction fqui admet une primitive
Fen admet en fait une infinit´e puisque F+ksera encore une primitive de f
quel que soit k∈R(ou mˆeme k∈Csi on consid`ere des fonctions `a valeurs
complexes). Cependant, ce sont les seules :
Propri´et´e : Soit fune fonction qui admet une primitive Fsur un inter-
valle I. Alors les primitives de fsont les fonctions de la forme F+kavec k
constante. De plus, si a∈I, alors fadmet une unique primitive qui s’annule
en I.
Remarque : ¸C a n ’ a d o n c p a s d e s e n s d e p a r l e r d e la primitive d’une fonction
fpuisqu’elle en a une infinit´e, mais ¸ca en a un de parler de la primitive de f
qui s’annule en a.
Consid´erons maintenant une fonction fqui admet une primitive Fsur
un intervalle Iet (a, b)∈I2.SiGest une autre primitive de fsur I
alors il existe une constante ktelle que G=F+k.DoncG(b)−G(a)=
(F(b)+k)−(F(a)+k)=F(b)−F(a). Donc l’accroissement de la primitive
entre aet bne d´epend pas de la primitive consid´er´ee, mais uniquement de la
fonction fet des nombres aet b.Onluidonneunnom:
D´efinition : Si fadmet une primitive Fsur un intervalle Iet si (a, b)∈I2,
alors on appelle int´egrale de fentre aet b, not´ee b
a
f(x)dx le nombre
F(b)−F(a).

7.1. TH ´ EORIE 51
Remarques :
–Sigest une fonction quelconque, on note [g(x)]b
ale r´eel g(b)−g(a). On
adoncb
a
f(x)dx =[F(x)]b
a.
–Ona
b
a
f(x)dx =−a
b
f(x)dx.
–Onsaitquelorsquel’onaunesomme,lenomdel’indicedesommation
ne change rien au r´esultat de la somme :
n
k=0
ak=
n
j=0
aj=
n
p=0
ap.De
mˆeme pour l’int´egrale, le nom de la variable intervenant dans l’intr´egale
n’intervient pas dans le r´esultat : b
a
f(x)dx =b
a
f(t)dt =b
a
f(u)du.
Attention cependant `a ne pas choisir comme nom de variable une des
bornes de l’int´egrale (i.e ´eviter b
a
f(b)db).
Exemples :
–10
6
(t3+5t)dt =1
4t4+5 2t210
6
=1
4104+5 2102−1 464+5 262=
2750 −414 = 2336.
–32
1
dt
t= [ln(t)]32
1= ln(32) −ln(1) = ln(32) = 5 ln(2).
–π/4
0
tan(x)dx =π/4
0
sin(x)
cos(x)dx =[−ln(cos(x))]π/4
0=1
2ln(2).
–π/2
0
(sin(x)+xcos(x))dx =[xsin(x)]π/2
0=π
2.
7.1.2 Propri´et´es de l’int´egrale
On va voir quelques propri´et´es calculatoires de l’int´egrale.
Soit fune fonction qui admet une primitive Fsur un intervalle Iet
(a, b, c)∈I3. Alors F(c)−F(a)=F(b)−F(a)+F(c)−F(b). Autrement
dit, on a la propri´et´e suivante :
Propri´et´e (relation de Chasles) : On a c
a
f(x)dx =b
a
f(x)dx+c
b
f(x)dx
(sous r´eserve d’existence des trois int´egrales).
De mˆeme, nous montrons :

52 CHAPITRE 7. CALCUL DE PRIMITIVE
Propri´et´e : L’int´egrale est lin´eaire :
b
a
(λf(x)+µg(x))dx =λb
a
f(x)dx +µb
a
g(x)dx
Propri´et´e : Si f0(resp. f0) sur un segment [a, b](et admet une
primitive), alors b
a
f(x)dx 0(resp.b
a
f(x)dx 0). De plus, si a<b
et que l’in´egalit´e est stricte sur f, alors l’in´egalit´e sur l’int´egrale est stricte
´egalement.
Exemple : Sans calculer de primitive (en admettant qu’il y en ait), on sait
que 1
0
earcsin(x)dx > 0.
Remarque : Les nombres aet bne sont pas quelconques : on doit avoir
ab,sinon,lessignesdesint´egralessontinvers´es.
Corollaire : On peut int´egrer les in´egalit´es entre aet bsi ab.
Propri´et´e (in´egalit´e triangulaire) : On a 
b
a
f(x)dx b
a|f(x)|dx
(sous r´eserve d’existence de ces int´egrales).
Exemple : Pour tout n∈N,ona:
1
0
cos3(x) sin2(x)xndx 1
0|cos3(x) sin2(x)xn|dx 1 0
xndx =1
n+1
On en d´eduit que 1
0
cos3(x) sin2(x)xndx →0quandn→∞et ce, sans faire
de calcul de primitives (en admettant que toutes ces fonctions en admettent).
7.1.3 Interpr´etations graphiques
Proposition. Soit fune fonction continue admettant une primitive sur
[a, b], alors il existe c∈[a, b]tel que
f(c)= 1
b−ab
a
f(t)dt.

7.2. CALCULS D’INT ´ EGRALES 53
Propri´et´e : Soit fune fonction continue sur I. Alors fadmet une (et donc
des) primitive(s) sur I. De plus si (a, x)∈I2, la valeur en xde la primitive
de fqui s’annule en aest l’aire comprise entre la courbe repr´esentative de
fet l’axe des abscisses sur l’intervalle [a, x](avec des conventions de signes).
Remarques :
–L’existencedelaplupartdesint´egralesestdoncquasi-automatique:`a
partir du moment o`u une fonction fest continue sur un intervalle [a, b],
on sait que b
a
f(x)dx existe.
–Lespropri´et´estellesquelarelationdeChaslesoul’int´egrationdesin-
´e g a l i t ´e s d e v i e n n e n t ´e v i d e n t e s s i o n l e s r e g a r d e e n t e r m e s d ’ a i r e s o u s l a
courbe.
Th´eor`eme (Th´eor`eme de Cauchy-Schwartz).Soit fet gdeux fonctions
continues sur [a, b], alors on a
b
a
f(t)g(t)dt2 ≤b
a
f2(t)dt b
a
g2(t)dt.
Egalit´e ssi ∃λ∈Rtel que f(x)=λg(x)(ou g≡0)∀x∈[a, b].
7.2 Calculs d’int´egrales
On va voir comment calculer des int´egrales dans certains cas lorsque l’on
ne dispose pas directement d’une primitive de la fonction `a int´egrer.
7.2.1 Int´egration par parties et changement de variable
Al’aidedespropri´et´esdelad´erivation(notammentleproduitetlacom-
position), on peut d´eduire des m´ethodes de calculs d’int´egrales :
Soient uet vdeux fonctions de classe C1sur un intervalle [a, b]. On a alors
(uv)�=u�v+uv�donc u�v=(uv)�−uv�.Commetouteslesfonctionssont
continues sur [a, b], on peut les int´egrer :
b
a
u�(x)v(x)dx =b
a
(uv)�(x)dx −b
a
u�(x)v(x)dx