Aucun titre de diapositive

1- Généralités
1.1- Notion de mouvements relatifs
Parler de mouvement d’un solide, de vitesse ou de trajectoire d’un point appartenant un solide n’a
de sens que si on défini par rapport à quoi on étudie le mouvement.
Exemple : On n e peut pas définir la trajectoire du centre de la lune, par contre on sait que la
trajectoire du centre de la lune par rapport à la terre se rapproche d’un cercle alors que le trajectoire du
centre de la lune par rapport au soleil se rapproche d’une épicyc loïde.
1.2- Définitions et notations
1.2.1- Orientation et vitesse de rotation
On appelle orientation d’un solide 1 par rapport au solide 2 l’angle entre un axe  X1fixe dans le
solide 1 et un axe  X2fixe dans le solide 2. On la note q1/2 .
On appelle vitesse de rotation du solide 1 par rapport au solide 2 la variation de l’orientation par
rapport au temps (C’est la dérivée de l’orientation par rapport au temps). On la note w1/2 et elle s’exprime
en radians par seconde : rad/s ou rad.s -1. On appelle fréquence de rotation du solide 1 par rapport au
solide 2 la vitesse de rotation exprimée en tours par minute : tr/min ou tr.min-1. On la note N1/2.
La relation entre vitesse de rotation et fréquence de rotation est : w1/2 = 2 . p. N1/2
60
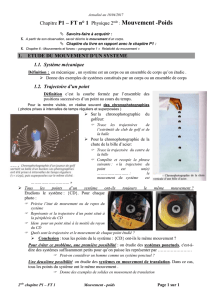
1.2.2- Trajectoire d’un point
On appelle trajectoire d’un point M appartenant au solide 1 par rapport au solide 2 la courbe décrite
par les points M au cours du temps dans un repère fixe par rapport au solide 2. On la note TM1/2 .

1- Généralités
1.2- Définitions et notations
1.2.3-Position et vitesse d’un point
On appelle position d’un point M appartenant au solide 1 par rapport au solide 2, le vecteur  O2Moù
O2est le centre d’un repère fixe dans le solide 2.
Cette vitesse est donc un vecteur noté :
On appelle vitesse d’un point M appartenant au solide 1 par rapport au solide 2 la variation de la
position de ce point M par rapport au temps. (C’est la dérivée du vecteur  O2M par rapport au temps).
VM1/2
1.2.4- Propriété de la vitesse par rapport à la trajectoire
Le vecteur  VM1/2 est toujours tangent à la trajectoire TM1/2.
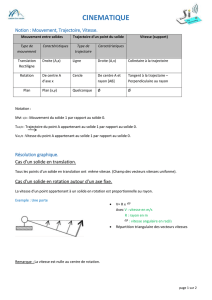
1.3- Les différents types de mouvements plan
Dans un problème plan, le mouvement d’un solide 1 par rapport à un solide 2 peut être :
- Une rotation : Dans ce cas il existe un point O, appelé centre de rotation, appartenant au solide
1 dont la vitesse par rapport au solide 2 est toujours nulle.  VO1/2 =  0
- Une translation : Dans ce cas l’orientation du solide 1 par rapport au solide 2 est toujours la
même. q1/2 = Constante w1/2 = 0
- Un mouvement plan quelconque : Dans ce cas il n’existe pas de point dont la vitesse est
toujours nulle et l’orientation du solide 1 par rapport au solide 2 n’est pas constante.

1- Mouvement de rotation
1.1- Liaison donnant un mouvement de rotation
Si les solides 1 et 2 sont en liaison pivot d’axe (O,  Z ) alors le mouvement de 1 par rapport à 2 est
un mouvement de rotation d’axe (0,  Z).
1.2- Liaisons équivalentes pour des problèmes plans
X
Y
O
1
2
Liaison pivot
d’axe (O,  Z )
X
Y
O
1
2
Liaison pivot glissant
d’axe (O,  Z )
X
Y
O
1
2
Liaison rotule
De centre O
X
Y
O
1
2
Liaison linéaire annulaire
D’axe (O,  Z )

1- Mouvement de rotation
1.3- Caractéristiques d’un mouvement de rotation
2
1O
M
Soit un solide 2 en rotation d’axe (O,  Z ) par rapport à un
solide 1, et w2/1 la vitesse de rotation de 2 par rapport à 1.
Alors, on a les caractéristiques suivantes :
- La trajectoire de M appartenant à 2 par rapport à 1 :
TM2/1 est un arc de cercle de rayon [OM]
- La vitesse de M appartenant à 2 par rapport à 1 :  VM2/1 est
perpendiculaire au rayon [OM] : 
VM2/1 ^[OM]
- Le module de la vitesse de M appartenant à 2 par rapport à 1 || VM2/1|| est :
||  VM2/1|| = |w2/1| . R où : R = OM et w2/1 en rad.s-1 .
- La vitesse du centre de rotation est nulle: 
VO2/1 =  0
TM2/1
VO2/1