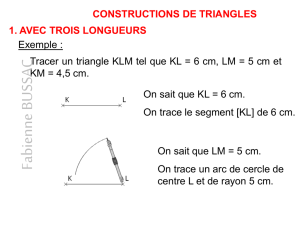
Le diaporama de la leçon

PROBABILITÉS
1. VOCABULAIRE
Lors du lancer d’un dé, on connaît tous les résultats
possibles, sans savoir, avant l’expérience, le résultat que
l’on va obtenir. Le résultat obtenu est dû au hasard.
On dit que c’est une expérience aléatoire.
Chaque résultat est appelé issue.
Un événement est constitué d’une ou plusieurs issues.
Fabienne BUSSAC

Exemple :
Lorsque l’on jette un dé, l’événement « On obtient 5 »
est constitué d’une seule issue :
L’événement «On obtient un nombre pair » est
constitué de trois issues :
Un événement constitué d’une seule issue est
appelé événement élémentaire.
Fabienne BUSSAC

2. NOTION DE PROBABILITÉ
a. Définition
Lorsqu’on effectue un très grand nombre de fois une
expérience aléatoire, la fréquence de réalisation d’un
événement se rapproche d’une fréquence théorique
appelée probabilité.
La probabilité qu’un événement A se réalise se note
p(A).
Fabienne BUSSAC

Exemples :
Si on lance une pièce un grand nombre de fois, on
obtient pile environ une fois sur deux : p(Pile) =
Si on lance un dé un grand nombre de fois, on obtient
5 environ une fois sur six : p(5) =
1
2
1
6
Fabienne BUSSAC

b. Propriété
La probabilité qu’un événement se réalise est un
nombre compris entre 0 et 1.
Un événement est appelé événement impossible s’il
ne peut pas se réaliser. Sa probabilité est égale à 0.
(exemple : obtenir 7 avec un dé.)
Un événement est appelé événement certain s’il se
réalise nécessairement. Sa probabilité est égale à 1.
(exemple : obtenir moins de 10 avec un dé.)
Fabienne BUSSAC