Repérage du plan - Académie en ligne

1
Séquence 2 – MA20
Séquence 2
Repérage dans le plan
Équations de droites
Sommaire
1. Prérequis
2. Repérage dans le plan
3. Équations de droites
4. Synthèse de la séquence
5. Exercices d’approfondissement
© Cned – Académie en ligne

3
Séquence 2 – MA20
1Prérequis
Repérage sur une droit graduée,
dans le plan repéré
Sur une droite
g
raduée, on peut repérer un point par son abscisse ; réci
p
ro
q
uement cha
q
ue nombre réel
corres
p
ond à un
p
oint de la droite,
p
oint dont il est l’abscisse
.
À savoir
 Sur l’axe gradué ci-dessous :
ABCOIDE
01
le point A a pour
absc
i
sse
( −3
)
,
le point B a pour abscisse ( −25
,
)
,
le point C a pour abscisse ( −1
)
,
le point D a pour abscisse ( 2
)
,
le point E a pour abscisse ( 4 25
,
)
environ.
 Sur l’axe gradué ci-dessous :
OI
0 0,5-2-3,5 2,6 5 1
E D C B A
le nombre 5 correspond au point A,
le nombre 2,6 corres
p
ond au
p
oint B,
le nombre 0,5 correspond au point C,
le nombre −2 corres
p
ond au
p
oint D
,
le nombre −3,5 correspond au point E.
A
Exemple
© Cned – Académie en ligne

4
Séquence 2 – MA20
Sur une droite graduée, on peut calculer la distance entre deux points dont on
c
onnaît les abscisses.
Pour calculer la distance entre A et B sur un axe, on e
ff
ectue la di
ff
érence entre
«
l’
a
b
scisse
l
a p
l
us gran
d
e » et «
l’
a
b
scisse
l
a p
l
us petite ».
À savoir
Sur l’axe gradué ci-dessous :
ABCOIDE
01
L
a distance DE est é
g
ale à :
DE "abscisse la plus grande" "abscisse la p=−llus petite"
"abscisse de E" "abscisse=−dde D" .=−=425 2 225
,,
L
a distance CD est égale à :
CD "abscisse la plus grande" "abscisse la p=−llus petite"
"abscisse de D" "abscisse=−dde C" .=−−
()
=213
L
a distance CA est égale à :
CA "abscisse la plus grande" "abscisse la p=−llus petite" .=−
()
−−
()
=143
L
a distance BO est égale à :
BO "abscisse la plus grande" "abscisse la p=−llus petite" .=−−
()
=02525 ,,
P
lan re
p
éré
Exemples
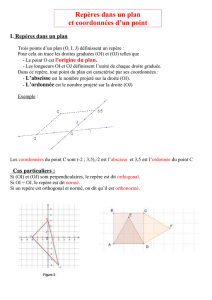
D
ans le plan ci-dessous, muni d’un repère
:
le point A a pour
a
bscisse
3
et pour ordonnée
1
,
5
;
le
p
oint B a
p
our abscisse (−2) et
p
our ordonnée 2,5 ;
le
p
oint C a
p
our abscisse (−1,5) et
p
our ordonnée 0 ;
le point D a pour abscisse (−1) et pour ordonnée (−2,5) ;
le point E a pour abscisse 0,5 et pour ordonnée
(
−0,75
)
environ.
Exemple
Dans le plan muni d’un repère ortho
g
onal, on peut repérer un point par son abscis
-
s
e et son ordonnée ; réci
p
ro
q
uement cha
q
ue cou
p
le de nombres réels corres
p
ond à
un
p
oint du
p
lan,
p
oint dont ce cou
p
le est le cou
p
le (abscisse ; ordonnée).
À savoir
© Cned – Académie en ligne

5
Séquence 2 – MA20
 Dans le même
p
lan ci-dessous :
le cou
p
le (2 ; −3) corres
p
ond au
p
oint F
;
le cou
p
le
(
1 ; 3
)
corres
p
ond au
p
oint G
;
le couple
(
0 ; −1,5
)
correspond au point H ;
le couple
(
−3 ; −3
)
correspond au point J ;
le couple (−1 ; 4) correspond au point K
.
G
E
F
H
J
D
C
A
B
K
01
1
Fonction affine, représentation
par une droite
 Fonction affine, re
p
résentation
p
ar une droit
e
D
ans le plan muni d’un repère ortho
g
onal, une fonction affine est représentée par une droite
.
V
oir s
é
quence 1
.
À savoir
B
© Cned – Académie en ligne

6
Séquence 2 – MA20
Figures de géométrie plane
Fi
g
ures particu
l
ières
Se souvenir des propriétés géométriques des figures particulières étudiées au col
-
l
ège : quadrilatères, triangles, cercles, polygones réguliers.
À savoir
Princi
p
aux théorèmes
Se souvenir des principaux théorèmes de géométrie étudiés au collège : théorème de
T
halès, réciproque de ce théorème, théorème de Pythagore, réciproque de ce théorème
.
À savoir
Tr
i
gonométr
ie
Se souvenir des dé
f
initions du cosinus d’un angle, de son sinus et de sa tangente, ainsi
q
ue des relations
q
ui les lient.
À savoir
Solides de géométrie dans l’espace
Solides
p
articuliers
Se souvenir des propriétés
g
éométriques des solides particuliers étudiés au collè
g
e :
p
arallélépipède rectan
g
le, prisme droit, c
y
lindre, p
y
ramides, cônes, sphères.
À savoir
C
D
© Cned – Académie en ligne