Exercices sur les fonctions x x ( ) = + 2 1 Exercice 2 (6 points) Soit f

Exercices sur les fonctions
Exercice 1
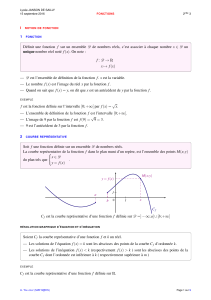
Soit la fonction f définie par f x x
x
( ) =+
2
1
.
1) Déterminer D
f
.
2) Calculer l'image de 3
4 et de 0.
3) Déterminer les antécédents éventuels de 0 de 1
3 et de 2.
4) Les points suivants sont-ils sur la courbe représentative de f : O(0;0) A(0;1) C(-1;-2) D(1;1) ?
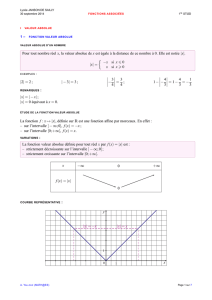
Exercice 2 (6 points)
Soit f la fonction définie sur [-2;2] dont on donne la courbe
représentative C
f
:
1) Déterminer graphiquement f( )
−
1 .
2) Trouver l’ensemble des images par f de tous les réels de
l’intervalle [0;2].
3) Résoudre graphiquement a) f x( )
=
−
2
b) f x( )
=
2
c) f x( )
≤
0
4) Dresser le tableau de variation de f sur [-2,2]
Exercice 3
Le plan est muni du repère orthonormal (O,i →,j →). Soit f la fonction
définie sur l'intervalle [-1;2] dont on donne la courbe représentative (C)
ci-contre.
1) Utiliser ce graphique pour déterminer les images de -1; 0; 1 et 2.
2) Dans quel intervalle varie f (x) lorsque x varie dans [-1;2] ?
3) Résoudre graphiquement a) f (x) = 0
b) f (x) < 0
4) Dresser le tableau de variation de f sur [-1;2] et indiquer pour quelle
valeur f admet un extremum (nature et valeur).
5) Construire dans le même repère la courbe C
g
, représentative de la
fonction g définie sur [-1;2] par : g (x) = -x +1
2.
6) Résoudre graphiquement a) f (x) = g (x)
b) f (x) ≥ g (x)
i →
2
O
-1
j →
C
f
-2
2
i →
O
j →
C
f

Exercice 4
Dans le repère ci−dessus, on a tracé la représentation graphique d'une fonction f définie sur l'intervalle
I = [ −2 ; 8 ]. Sans justifier vos réponses, utiliser les informations du dessin pour répondre aux questions
suivantes :
1) Quel est le maximum de f sur I ?
2) Quel est le minimum de f sur I ?
3) Quelle est l'image de
3
4
?
4) Quels sont les antécédents de 1 ?
5) Sur quels intervalles f est-elle strictement croissante ?
6) Sur quels intervalles f est-elle strictement décroissante ?
7) Sur quels intervalles f est-elle constante ?
8) Pour quelles valeurs de x∈I a-t-on f(x) = 0 ?
9) Pour quelles valeurs de x∈I a-t-on f(x) = 2 ?
10) Pour quelles valeurs de x∈I a-t-on f(x) < 0 ?
11) Pour quelles valeurs de x∈I a-t-on f(x) ≥ 1 ?
12) Pour quelles valeurs de x∈I a-t-on f(x) ≥ 2 ?
Exercice 5
ABCD est un carré de côté 1. Le point M appartient au segment [AB].
On pose BM = x. M' est le point d'intersection entre l'arc de cercle de centre C et de rayon 1 et le segment [CM' ]
comme sur la figure ci-contre.
1) A quel intervalle I appartient x ?
On définit la fonction f sur I par f(x) = MM'.
2) Déterminer géométriquement le sens de variation de f sur I.
3) Quelle est la distance CM' ?
En déduire l'expression de f(x) en fonction de x.
A
B
C
D
M
M'

Exercice 6
La courbe ci-dessous est donnée dans un repère orthogonal et (C) est la courbe représentative d'une fonction f
définie sur l'intervalle [-2;2].
O 1
1
2
2
3
-2 -1
-1
.
.
.(C)
Partie A
1) A l'aide de la courbe (C) représentative de la fonction f, recopier et compléter le tableau de valeurs ci-après par
lecture graphique :
x -2 -1 0 1 2
f(x)
2) a) Donner, s'il(s) existe(nt) les antécédents de -4 et de 0.
b) Quels sont les nombres qui ont pour image 1, pour image 3 ?
Partie B
La courbe représentée par le graphique ci-dessus est celle de la fonction f définie sur l'intervalle [-2;2] par f(x) = x
3
-
3x + 1.
1) Déterminer par le calcul les images de -1 et de 2 par f.
2) Déterminer par le calcul les solutions de l'équation f(x) = 1 et retrouver un des résultats de la partie A.

Exercice 7
Le directeur d'un cirque sait que le nombre de spectateurs par séance est fonction du prix de la place ; il veut fixer
ce prix à un nombre entier d'euros et s'assurer une
recette maximale. Il sait qu'il reçoit en moyenne 500
spectateurs par séance lorsque le prix de la place est
fixé à 19€. Mais à chaque fois qu'il baisse le prix de la
place de 1€, il a 80 spectateurs de plus.
1) Lequel de ces deux graphiques représente le mieux
la recette en fonction de la baisse de prix ?
2) Déterminer graphiquement de combien il doit
baisser le prix pour avoir une recette maximale.
3) Soit n le nombre d'euros dont le prix baisse.
a) Quelles sont les valeurs que peut prendre n ?
b) Montrer que la recette est
(19 - n)×(500 + 80×n).
c) Déterminer à l'aide de la calculatrice le prix pour
lequel la recette est maximale.
0
2000
4000
6000
8000
10000
12000
14000
0 2 4 6 8 10 12 14 16 18 20
0
2000
4000
6000
8000
10000
12000
14000
0 2 4 6 8 10 12 14 16 18 20