Principe_Sédimentation

Daniel Huilier IMFS Equipe Instabilités-Turbulence-Diphasique
Vitesse de Sédimentation particulaire
Pour des particules de masse m, de masse volumique ρP, de volume V tombant ou remontant à une vitesse
constante U dans un fluide au repos de masse volumique ρF la force de traînée induite par la répartition de
pression statique et les forces visqueuses contrebalance l’effet de la force de gravité (le poids mg) et de la
poussée d’Archimède.
gVSUC FPFD )(
2
12
ρρρ −=
Pour une sphère de diamètre D : S= π.D2/4 et V = πD3/6
Et on définit alors un nombre de Reynolds sans dimension Re = U.D/ν , où ν est la viscosité cinématique du
fluide
L’analyse dimensionnelle révèle que le coefficient de traînée CD ne dépend que du nombre de Reynolds Re.
On montre facilement que :
3*2
3
4
Re DCD=
où
3/1
2
*)1(
.⎥
⎦
⎤
⎢
⎣
⎡−
=
ν
gs
DD et un diamètre sans dimension et
F
P
s
ρ
ρ
=densité relative
Pour des particules de Stokes (Re «1): Re
24
=
D
C
Un lissage empirique de Schiller and Naumann, 1933, (pour Re < 800) donne :
687.0
DRe)15.01(
Re
24
C+=
Variables
CD = coefficient de traînée
U = vitesse de sédimentation (settling velocity)
D = particle diameter
S = Surface projetée de la particule (particle projected area )
V = volume de la particule
g = acceleration due to gravity
ν = viscosité cinématique du fluide
References
Cheng, N.-S., 1997, A simplified settling velocity formula for sediment particles, ASCE J. Hydraulic Engineering, 123, 149
1

Daniel Huilier IMFS Equipe Instabilités-Turbulence-Diphasique
Vitesse de sédimentation
Cas des faibles nombres de Reynolds, particules à comportement Stokien
Equation du mouvement d’une particule dans un fluide de vitesse :
f
u
2
4
3
1r
D
p
f
p
fp u
D
C
g
dt
du
ρ
ρ
ρ
ρ
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−= où fpr uuu
−
=
est la vitesse de glissement de la particule
Dans un fluide au repos est nul.
f
u
A l’équilibre, dans un fluide au repos 0,
=
=fpr uuu
0
4
3
12=−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−= r
D
p
f
p
fp u
D
C
g
dt
du
ρ
ρ
ρ
ρ
Et la vitesse terminale U de la particule vaut :
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−= 1
3
4
f
p
D
C
D
gU
ρ
ρ
Pour des nombre de Reynolds particulaires faibles 1/Re
<
=
μ
ρ
fr
Du
Re
24
=
D
C et la force de traînée est r
DuF
πμ
3= traînée dite visqueuse, due à la couche limite laminaire et à
la répartition de pression autour de la sphère :
)(
18
2
fp
gD
U
ρρ
μ
−=
Exemple de vitesse de chute terminale d’une sphère de verre (ρp = 2500kg/m3) tombant dans de l’air (ρf = 1,2
kg/m3, μ = 1,7 10-5 kg/ms) :
D = 50 μm → U = 0,20 m/s, Re = 0,71 dominance visqueuse
D = 500 μm → U = 17,59 m/s, Re = 6209 dominance inertielle
2

Daniel Huilier IMFS Equipe Instabilités-Turbulence-Diphasique
Coefficient de traînée CD
Pour les écoulements à grand nombre de Reynolds on introduit souvent le coefficient de traînée CD (sans
dimension). La force de traînée est définit par
DD SCUF 2
2
1
ρ = , CD = f(Re) où Re = UD/ν est le nombre de Reynolds et S = πR2
où S est la section de l’objet et FD la force de traînée (drag en anglais, d’où le sigle D). En identifiant le
coefficient de traînée avec l’expression de la force de Stokes DUFD
πμ
3
=
, on trouve :
Re
24
=
D
C
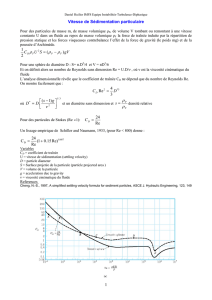
où le nombre de Reynolds Re est calculé sur le diamètre (D = 2R) de la sphère. La figure ci-dessous montre
que l’expression de la force de Stokes est une bonne approximation de la force de traînée jusqu’à Re ~ 1.
Au delà, la correction analytique d’Oseen permet d’écrire à l’ordre suivant (Re ≤ 5) :
⎟
⎠
⎞
⎜
⎝
⎛+= Re
16
3
1
Re
24
D
C
A plus haut nombre de Reynolds encore on peut trouver d’autres formules empiriques pour CD.
Traînée sur une sphère à faible nombre de Reynolds (attention CD est ici multiplié par π/4).
D’après la référence D. J. Tritton. Physical fluid dynamics. (second edition), Oxford University Press, 1988.
3

Daniel Huilier IMFS Equipe Instabilités-Turbulence-Diphasique
Une sphère unique placée dans un fluide va sédimenter si sa densité est supérieure à la densité du fluide.
Après une phase initiale d’accélération, elle va ensuite sédimenter à sa vitesse limite de chute. La valeur du
nombre de Reynolds calculé avec cette vitesse de chute va permettre de savoir si c’est un vitesse de chute
visqueuse ou inertielle. Dans le premier cas il y a égalité entre le poids apparent (poids corrigée de la poussée
d’Archimède) et la force de Stokes :
StokesFS RURg
πμπρρ 6
3
4
)( 3=−
soit 2
.
9
2R g
UStokes
μ
ρ
Δ
=
avec FS
ρ
ρ
ρ
−=Δ . Cette vitesse limite de chute est dite vitesse limite de Stokes. Elle est proportionnelle
au carré du rayon, donc les grosses particules sédimentent plus vite. Ce résultat reste vrai même si les
particules ne sont pas parfaitement sphériques.
En réalité, les toutes petites particules (~ 1 μm) dites particules colloïdales ou particules browniennes ne
sédimentent pratiquement pas à cause de l’agitation thermique (la vitesse aléatoire moyenne devient
supérieure à la vitesse de sédimentation).
Pour que le nombre de Reynolds de chute soit petit et que l’on puisse utiliser la formule de la force de Stokes
il faut :
1..
9
4
2
Re 2
3
<<
Δ
==
νρ
ρ
ν
gR
RUStokes
soit
3
1
2
..
4
9⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
Δ
<< g R
ν
ρ
ρ
Si maintenant beaucoup de particules sédimentent ensemble, le calcul de la vitesse de sédimentation se
complique nettement (il n’est d’ailleurs pas résolu à ce jour). En effet il existe des interactions collectives (à
N corps) car le champ de vitesse autour d’une particule décroît lentement (en 1/r) et des effets dus à la taille
finie du récipient (effet de paroi). De fait la sédimentation d’un grand nombre de particules crée un contre-
écoulement du fluide vers le haut qui ralentit leur chute (une jolie démonstration en est l’effet Boycott
observé lorsque l’on incline le récipient). La vitesse est alors une fonction de la concentration en particules :
– A faible Reynolds, Albert Einstein (1905) a donné le premier terme correctif à la vitesse limite de chute
dépendant de la concentration c en particules : Vlim ≈ VStokes [1 − 6, 55 c].
– Au-delà, on utilise la loi empirique de Richardson-Zaki, Vlim ≈ VStokes [1 − c/cmax]n où n ≈ 5, mais dépend
du nombre de Reynolds et cmax est la compacité maximum, de l’ordre de 54 % pour un empilement
aléatoire lâche de sphères identiques.
4

Daniel Huilier IMFS Equipe Instabilités-Turbulence-Diphasique
Extrait du projet Face de l’Institute of Energy Technology (Lasse Rosendahl, Aalborg University)
Dans un fluide au repos
2
4
3
1P
D
p
f
p
f
Pu
D
C
g
dt
du
ρ
ρ
ρ
ρ
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−=
Si le nombre de Reynolds est faible,
fP
DDu
C
ρ
μ
24
Re
24 == et la force de traînée est P
DuF
πμ
3=,
et
P
P
p
f
P
pp
f
P
D
p
f
p
f
Pu
gu
D
gu
D
C
g
dt
du
τρ
ρ
μ
ρρ
ρ
ρ
ρ
ρ
ρ
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−=−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−=−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−= 1
18
1
4
3
12
2
La vitesse de chute limite est )(
18
2
fp
gD
U
ρρ
μ
−= et le temps de relaxation
μ
ρ
τ
18
2
D
P
P=
L’équation du mouvement s’écrit :
P
P
P
Pu
U
dt
du
ττ
−=
Cette équation différentielle linéaire a pour solution :
[
]
)/exp(1( PP tUu
τ
−
=
si la particule a une vitesse nulle au départ (t = 0, uP = 0)
5