Corrigé de l`interrogation n°3 - IMJ-PRG

CORRIG´ E DE L’INTERROGATION NUM´ ERO 3
Exercice 1. Soit f:E→Fune application, Aet Bdeux sous-ensembles de E.
Montrons d’abord que f(A∪B)⊆f(A)∪f(B). Soit y∈f(A∪B). Par d´efinition,
il existe x∈A∪Btel que f(x) = y. Par d´efinition de l’union, soit xappartient `a
A, soit xappartient `a B. Dans le premier cas, y=f(x) appartient `a f(A), et dans
le second cas, yappartient `a f(B). Dans les deux cas, y∈f(A)∪f(B).
Montrons ensuite que f(A)∪f(B)⊆f(A∪B). Soit donc y∈f(A)∪f(B).
Si yappartient `a f(A), par d´efinition, il existe x∈Atel que f(x) = y. Puisque
A⊆A∪B,x∈A∪B, donc y=f(x) appartient `a f(A∪B). De mˆeme, si y∈f(B)
on montre que y∈f(A∪B).
Exercice 2. Soit f:E→Fune application entre deux ensemble, et f∗:P(E)→
P(F) la fonction qui, `a un sous-ensemble Ade E, associe son image directe par f,
f(A). Montrons que, si fest injective, alors f∗est injective.
On suppose donc que fest injective. Soient A, B ∈ P(E) tels que f∗(A) = f∗(B).
On va montrer que A=B.
Soit xun ´el´ement de A. Alors f(x) appartient `a f(A). Or f(A) = f∗(A) = f∗(B) =
f(B). Donc f(x) appartient `a f(B). Il existe donc y∈Btel que f(y) = f(x). Puisque
fest injective, on en d´eduit que x=y. Donc xappartient `a B. On a prouv´e que
A⊆B, et on montre de mˆeme que B⊆A.
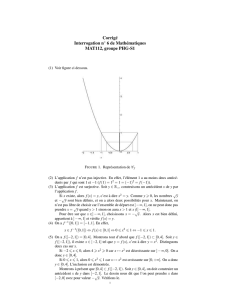
Exercice 3. a) ´ Etudions la fonction :
f:R→R
x7→ x2
fn’est pas injective. En effet on v´erifie par exemple que −1 et 1 ont la mˆeme
image par f.fn’est pas non plus surjective. En effet les nombres strictement
n´egatifs n’ont pas d’ant´ec´edent par f.
b) ´ Etudions la fonction g, restriction de f`a [0; +∞[. gest injective. Par exemple
parce qu’elle est strictement croissante. On peut aussi v´erifier que, si y∈R,
alors soit yest positif, auquel cas le seul ant´ec´edent positif de ypar gest √y,
soit yest n´egatif, auquel cas yn’a pas d’ant´ec´edent. Et pour cette derni`ere
raison, gn’est pas surjective.
c) ´ Etudions la fonction :
f:R→[0; +∞[
x7→ x2
hn’est pas injective. −1 et 1 sont tous deux envoy´es sur 1 par h.hest
surjective. En effet, pour tout r´eel positif y,√yest un ant´ec´edant de ypar
f.
d) ´ Etudions la fonction k, restriction de h`a [0; +∞[. kest injective, par exemple
parce qu’elle est strictement croissante, ou encore parce que tout r´eel positif
admet pour seul ant´ec´edent par hle r´eel positif √y. Pour la mˆeme raison, k
est surjective. Donc kest bijective.
1