THÈME 1

THÈME 1: STATISTIQUES 1 livre pages 145 3°
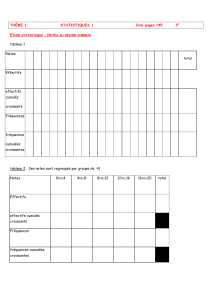
ETUDE STATISTIQUE : NOTES AU DEVOIR COMMUN
tableau 1
Notes
total
Effectifs
effectifs
cumulés
croissants
Fréquences
fréquences
cumulées
croissantes
tableau 2 : (les notes sont regroupés par groupe de 4)
Notes
0<n4
4<n8
8<n12
12<n16
16<n20
total
Effectifs
effectifs cumulés
croissants
Fréquences
fréquences cumulées
croissantes

RAPPELS
1- VOCABULAIRE :
La population étudiée est la classe de troisième 6
Le caractère étudié pour cette population est la note au devoir commun (un caractère est quantitatif ou qualitatif)
Les individus composant la population sont les élèves de troisième
On regroupe les individus par classe :
Il peut s’agir d’une note (exemple 1) ou d’un intervalle de notes (exemple2)
L’effectif d’une classe est le nombre d’individus de cette classe.
L’effectif total est le nombre total d’individus.
La fréquence d’une classe est le quotient de l’effectif de cette classe par l’effectif total.
Elle est parfois exprimée en pourcentage. Parfois elle est arrondie.
La fréquence totale est égale à 1 (ou 100 si exprimée en pourcentage). Parfois la somme des fréquences ne donne
pas exactement 1 (ou 100) en raison des arrondis.
2- REPRESENTATIONS GRAPHIQUES :
à partir du tableau 1 : Diagramme en bâtons (ou à barres)
à partir du tableau 2 : Histogramme Diagramme circulaire (ou semi-circulaire)
3-EFFECTIFS CUMULES ET FREQUENCES CUMULEES
Pour le tableau 1 :
L’effectif cumulé croissant d’une note est le nombre d’individus ayant une note inférieure ou égale à cette
dernière : pour le trouver il suffit d’additionner les effectifs des notes inférieures et d’ajouter l’effectif de la
note concernée.
Même type de définition pour la fréquence cumulée croissante. Pour la calculer on peut ajouter les fréquences
(mais risque d’erreurs si elles sont arrondies) ou faire le quotient de l’effectif cumulé croissant correspondant par
l’effectif total.
4-MOYENNE
La moyenne de la classe (tableau 1) au devoir commun se calcule :
1) soit en ajoutant toutes les notes des devoirs et en divisant par le nombre de devoirs (effectif total de la
population)
La moyenne de la classe à partir du tableau 2 se fait par la méthode 2, en choisissant comme note pour chaque
classe le centre de cette classe :
2) soit en multipliant l’effectif d’une classe par le centre de la classe, en faisant la somme puis diviser par l’effectif
total. (Chaque note est pondérée par l’effectif correspondant).

COURS
1- ÉTENDUE D’UNE SERIE STATISTIQUE :
C’est la différence entre la valeur la valeur la plus grande de la série et la valeur la plus petite.
 Exemple : série des scores obtenus par les sept joueurs de l’équipe des Verts:
105—120—104—121 —99 —127- 108
Dans cet exemple : 127 – 99 = 28
On dit que l’étendue d’une série statistique est une caractéristique de dispersion, qui permet de comparer
des séries qui auraient des valeurs moyennes et/ou médianes proches.
2- VALEUR MEDIANE D’UNE SERIE STATISTIQUE :
On appelle médiane M d’une série statistique de N données rangées dans l’ordre croissant, tout nombre qui
partage cette série ordonnée en deux sous séries de même effectif.
 Si N est impair, la médiane est la valeur centrale de la série.
 Si N est pair, la médiane est la moyenne des « deux données centrales » de la série.
 On dit que la médiane d’une série statistique est une caractéristique de position.
Cette série statistique porte sur l’âge des joueurs de l’équipe de France de, football championne d’Europe en 2014 :
Âge
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
TOTAL
Effectif
0
1
2
0
1
0
4
0
3
4
1
2
2
0
1
1
22
La valeur médiane est la valeur (de l’âge) qui se trouve au « MILIEU » de la série, qui la partage en deux
séries d’effectif égal.
Réécrivons tous les âges par ordre croissant : puis séparons le nombre de valeurs en 2 groupes de même
effectif : (on divise l’effectif total par 2: 22 :2=11) est entre la 11ème et la 12ème donnée
21 22 22 24 26 26 26 26 28 28 28 29 29 29 29 30 31 31 32 32 34 35
11 joueurs Médiane = 28,5 11 joueurs
La médiane de cette série statistique est de 28,5 ans.
Remarques :
- Dans le cas où l’effectif de la série est impair, la « ligne de partage » est située juste sur une valeur : C’est
la valeur médiane.
- Dans le cas où l’effectif de la série est pair (dans notre exemple), la « ligne de partage » est située juste
entre deux valeurs de la série. Si ces deux valeurs sont différentes, on prend leur moyenne pour valeur
médiane.

3- QUANTILES D’UNE SERIE STATISTIQUE :
Les quantiles sont des valeurs qui partagent une série en parties égales :
Les quartiles partage la série en en 4 parties égales.
 Le premier quartile (noté Q1 ) d’une série ordonnée dans l’ordre croissant est la plus petite valeur de cette
série pour laquelle au moins un quart ( 25%) des valeurs sont inférieures ou égales à Q1 .
 Le troisième quartile (noté Q3 ) d’une série ordonnée dans l’ordre croissant est la plus petite valeur de cette
série pour laquelle au moins trois quarts ( 75% ) des valeurs sont inférieures ou égales à inférieure ou égale à Q3 .
 La différence Q3  Q1 s’appelle écart interquartile.
Réécrivons tous les âges par ordre croissant :
Pour déterminer Q1, on calcule le quart de l’effectif :
1
4
effectif (on divise le nombre de valeurs par 4). On
obtient le rang du premier quartile.
Pour déterminer Q3, on calcule les trois quarts de l’effectif :
3
4
effectif, on obtient le rang du troisième quartile.
Dans le cas où le résultat n’est pas une valeur entière, on arrondit à la valeur entière par excès.
L’effectif = 22 (22 valeurs dans la série);
Rang du 1er quartile : 22 4 = 5,5 donc la 6ème valeur correspondra au 1er quartile
Donc Q1 = 26
Et
Rang du 3ème quartile : 3 (224)= 16,5 donc la 17ème valeur correspond au troisième quartile
Donc Q3 = 31
21 22 22 24 26 26 26 26 28 28 28 28 29 29 29 30 31 31 32 32 34 35
1er quartile 3 ème quartile