STATISTIQUES

STATISTIQUES
1. Un peu de vocabulaire
Faire une étude statistique, c’est étudier, pour une population donnée, un caractère des
éléments de cette population. L’effectif est le nombre d’éléments de cette population.
Exemples
Population
Effectif
Caractère étudié
EX1 : Classe de 3ème C
27
moyenne en maths
EX2 : Classe de 3ème C
27
couleur des yeux
EX3 : Voitures vendues en
France en 2003
2!009!254
marque de la voiture
Les exemples 1 et 2 montrent que le caractère étudié peut-être :
— quantitatif ( la note est une mesure c’est à dire un nombre )
— qualitatif ( la couleur des yeux ne se mesure pas par un nombre )
L’exemple 3 montre qu’une population statistique peut être formée par autre chose que des
personnes ( ici, c’est une population de voitures )
Une étude statistique commence souvent par un sondage.
L’organisme le plus souvent cité est l’INSEE :
INSEE : Institut National de la Statistique et des Etudes Economiques.
Ensuite, les données récoltées sont analysées sur ordinateur par des logiciels appropriés.
2. Représentation graphique d’une série statistique
A) Diagramme circulaire ( appelé camembert )
En général, on emploie ce diagramme
lorsque le caractère étudié est qualitatif.
L’angle des secteurs circulaires
est proportionnel aux effectifs de la série.
Yeux bleus
Yeux noirs
Yeux marrons
Total
Effectifs
Fréquences
Pourcentages
Angles

B) Diagramme en barres ( appelé histogramme )
On l’emploie lorsque le caractère étudié est quantitatif et continu.
Exemple : moyenne en maths de la 3ème E ( 26 élèves )
La moyenne peut être n’importe quel nombre compris entre 0 et 20. Il y a continuité de 0 à 20.
La hauteur des barres
est proportionnelle aux effectifs.
C) Diagrammes en bâtons ( avec ou sans épaisseur )
On l’emploie quand le caractère étudié est quantitatif sans être continu.
Exemple 4 : Nombre d’animaux domestiques ( chiens et chats ) dans les familles des élèves.
La hauteur des bâtons
est proportionnelle aux effectifs.
Moyenne M
0 ≤ M ≤ 4
4 < M ≤ 8
8 < M ≤12
12 < M ≤ 16
16 < M ≤ 20
Faible
Insuffisant
Moyen
Bien
Très bien
Effectifs
1
2
14
3
6
Fréquences
1/26
2/26
14/26
3/26
6/26
Pourcentages
4"%
8"%
54"%
11"%
23"%
15
10
5
0
1 2 14 3 6
Moyennes
Faible
Insuffisant
Moyen
Bien
Très bien
Nbre animaux
0
1
2
3
Total
Effectifs
5
15
4
2
26
Fréquences
5/26
15/26
4/26
2/26
1
Pourcentages
19"%
58"%
15"%
8"%
100"%
15
10
5
0
E
f
f
e
c
t
i
f
s
5
15
4
2
Nombre animaux
0 1 2 3
Classe de 3ème1

3. Utilisation des pourcentages
Voici les résultats des moyennes trimestrielles de deux classes imaginaires A et B.
Le professeur juge que le trimestre est réussi à partir d’une moyenne de 12.
Quelle est la classe qui a réussi le mieux ?
Dans la classe A, 14 élèves ont bien réussi mais c’est 14/ 20 !
Dans la classe B, 16 élèves ont bien réussi mais c’est 16 /25 !
On ne peut pas juger avec un effectif total différent.
En utilisant des pourcentages, on va faire comme si il y avait 100 élèves dans chaque classe.
Finalement, contrairement aux apparences, c’est la classe A qui obtient la meilleure réussite.
Conclusion : Quand, pour un même caractère étudié, on veut comparer deux populations, on
calcule les fréquences en pourcentage.
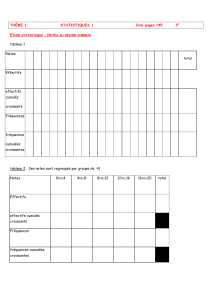
4. Moyenne, effectifs cumulés croissants et étendue d’une série statistique.
A) Moyenne
Voici la série de 5 notes sur 20, obtenus par Philippe et Anne.
Philippe Anne
Moyenne Moyenne
M = ( 16 + 10 + 11 + 12 + 28 ) / 7 M = ( 8 + 5 + 12 + 16 + 36 ) / 7
= 11 = 11
Les deux élèves n’ont pas le même profil.
Non, les notes de Philippe sont plus resserrées que celles de Anne.
Conclusion : La moyenne, toute seule n’apporte pas beaucoup d’information.
B) Etendue d’une série statistique
L’étendue d’une série statistique est l’écart entre les deux valeurs extrêmes de la série.
Pour Philippe, l’étendue est : 14 – 8 = 6 ( ses notes sont “ regroupées “ )
Pour Anne, l’étendue est 18 – 4 = 14 ( ses notes sont plus dispersées )
Conclusion : L’étendue d’une série statistique apporte une information complémentaire.
Moyenne M
0 ≤ M ≤ 4
4 < M ≤ 8
8 < M ≤12
12 < M ≤ 16
16 < M ≤ 20
Faible
Insuffisant
Moyen
Bien
Très bien
Effectifs de A
1
0
5
11
3
Effectifs de B
1
2
6
12
4
%
5
0
25
55
15
%
4
8
24
48
16
Notes
8
10
11
12
14
Coefficients
2
1
1
1
2
Notes
4
5
12
16
18
Coefficients
2
1
1
1
2

C) Effectifs cumulés croissants
Voici les notes obtenues par une classe de 20 élèves
Pour chaque valeur de la série, on cumule les effectifs des valeurs inférieures ou égales
Ainsi, par exemple, on voit aussitôt sur la ligne des effectifs cumulés qu’il y a 9 élèves qui
n’ont pas obtenu la moyenne.
Cette ligne peut être intéressante pour faire le bilan de la classe.
5. Médiane, premier et troisième quartile d’une série statistique.
D) Médiane d’une série statistique
Définition :
Les valeurs de la série étant rangées par ordre croissant, la médiane d’une série
statistique est une valeur qui partage cette série en deux parties de même effectif.
Exemple 1 : Il y a un nombre impair de notes ( 11 notes par exemple )
11 = 2 x 5 + 1 ( la médiane est la 6
ème valeur )
5 valeurs la médiane est 13 5 valeurs
Exemple 2 : Il y a un nombre pair de valeurs ( 6 notes par exemple )
6 = 2 x 3
3 notes 3 notes 3 notes 3 notes
La médiane est 11 La médiane est 12,5
3 ème note = 4 ème note 12,5 = ( 11 + 14 ) / 2
Pour calculer la médiane :
— on range les valeurs de la série par ordre croissant
— si l’effectif est impair ( 2n + 1 ) alors la médiane est la ( n + 1 )ème valeur
— si l’effectif est pair ( 2n ) alors la médiane est la moyenne entre la nème et la ( n + 1 )ème
valeur.
Notes
2
5
6
9
12
13
15
16
18
20
Effectifs
1
3
2
3
2
1
4
1
2
1
Effectifs cumulés
croissants
1
4
6
9
11
12
16
17
19
20
5
5
11
12
13
13
15
16
16
17
20
8
10
11
11
12
13
8
10
11
14
15
16

E) Premier quartile
Définition
Les valeurs de la série étant rangées par ordre croissant, le premier quartile est la valeur Q1
pour laquelle au moins 25% des valeurs sont inférieures ou égales à Q1.
Exemple 1
Effectif : 14 14 : 4 = 3,5
Le premier quartile est donc la 4ème note c’est à dire 9.
Au moins 25% des élèves ont une note inférieure ou égale à 9.
Exemple 2
Effectif : 16 et 16 : 4 = 4
Le premier quartile est la 4ème note c’est à dire 5.
Au moins 25% des élèves ont une note inférieure ou égale à 5.
F) Troisième quartile
Définition
Les valeurs de la série étant rangées par ordre croissant, le troisième quartile est la valeur Q3
pour laquelle au moins 75% des valeurs sont inférieures ou égales à Q3.
Exemple 1
Effectif : 14 14 : 4 = 3,5 et 3,5 x 3 = 10,5
Le troisième quartile est donc la 11ème note c’est à dire 16.
Au moins 75% des élèves ont une note inférieure ou égale à 16.
Exemple 2
Effectif : 16 et 16 : 4 = 4 et 4 x 3 = 12
Le troisième quartile est donc la 12ème note c’est à dire 15.
Au moins 75% des élèves ont une note inférieure ou égale à 15.
5
5
8
9
10
10
14
15
15
15
16
17
18
18
1
3
5
5
5
9
10
10
14
15
15
15
16
17
18
18
5
5
8
9
10
10
14
15
15
15
16
17
18
18
1
3
5
5
5
9
10
10
14
14
15
15
15
17
18
18