Sinus et Cosinus sont dans un bateau (tangente et cotangente les

Sinus et Cosinus sont dans un bateau (tangente et cotangente les suivent) ...
Ou comment, à l'aide de la trigonométrie, couper une tarte en 6 portions égales,
sans rapporteur et sans équerre (ou presque)
INTRODUCTION :
Voici une magnifique tarte coupée en 6 parts égales !
Mais comment parvenir à ce découpage régulier sans rapporteur ou appareil de mesure complexe ?
Observons de plus près, et remarquons certaines lignes particulières...
On constate que les points de coupe sur le pourtour de la tarte sont obtenus à partir :
-d'abord d'un diamètre (en vert)
-puis de perpendiculaires issues du milieu des rayons (pointillés rouges)
Donc, pour couper une tarte en 6, il suffit de "viser le milieu d'un rayon, projeter orthogonalement ce point
sur le cercle et ensuite couper à partir de ce point, en passant par le centre !" Simple, non ?
Mais voyons ce que cela donne en langage trigonométrique...

y
O
A
x
M
P
E
G
H
Z
Derrière ces noms de sinus, cosinus, ... se cachent des valeurs numériques, très précises.
Ces valeurs ont un rapport étroit avec les angles ; et pour mieux comprendre, rappelons-nous qu'elles sont liées
au théorème de Pythagore (qui s'intéresse particulièrement aux triangles rectangles).
On peut mettre un visage sur ces nombres en utilisant le cercle trigonométrique (un cercle dont deux
diamètres perpendiculaires forment avantageusement un repère orthonormé, pour peu qu'on y précise l'unité).
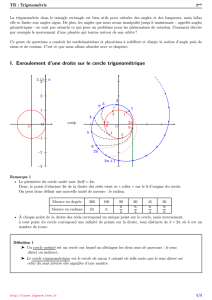
Soit, donc, un cercle de centre O et de rayon 1 (unité, mètre, kilomètre, ce qu'on veut...), dans lequel on a tracé un
angle α, issu de O et ayant pour côtés [Ox) et [OA).
Nous avons donc un triangle OAM, rectangle en M et A étant le point d'intersection entre (OA) et le cercle..
M et P sont les projetés orthogonaux de A sur, respectivement (Ox) et (Oy) .
Puisque le rayon de ce cercle est égal à 1 (unité), nous avons, en appliquant Pythagore (à partir de l'angle OMA),
OM² + AM² = OA² , soit en simplifiant,
OM² + AM² = 1
Mais un esprit avisé remarquera que, étant dans un repère orthonormé,
AM = OP, d'où cette nouvelle égalité :
OM² + OP² = 1 (Pythagore vu sous l'angle POM)
1
Bien, mais sinus, cosinus, tangente et cotangente, dans tout ça ?
Regardons bien notre schéma:
Sinus(α) sera la valeur OP, -1  OP +1
cosinus(α), sera la valeur OM , -1 OM +1
tangente(α), sera la valeur xG, avec (xG)(Ox).
cotangente(α) (par analogie entre sinus et cosinus)
sera la valeur yE, avec (yE) (Oy).
Par calculs, on peut également obtenir les égalités suivantes :
Sin(α) = OP = AM
Cos(α)= OM = AP
Tg (α) = xG = AH
Cotg(α)= yE = AZ
Et ma tarte, alors ?
Patience...
1
Comme la tarte... aux pommes!

Avant cela, il nous faut regarder de plus près ce cercle trigonométrique et quelques unes de ses valeurs
remarquables, obtenues par calcul, toujours d'après Pythagore.
On sait que tout ce qui a rapport au cercle utilise de près ou de loin le nombre Pi ().
La circonférence d'un cercle s'obtient par le calcul 2 x  x R (R étant le rayon de ce cercle).
Dans le cas qui nous préoccupe, cette circonférence est donc égale à: 2 x  x 1, donc 2 . Il est donc logique de
"découper" ce cercle en subdivisions de  ou 2 .
Le cercle ci-dessous nous donne alors quelques valeurs remarquables des sinus et cosinus. Les  et 
disséminées de-ci de-là sont dues aux calculs effectués à partir du théorème de Pythagore.
Sur ce schéma, je remarque en particulier que pour un angle de 60°, soit 
, la valeur du cosinus est égale à 0,5 .

Je vais pouvoir me servir de ce résultat-là pour couper ma tarte !
Couper une tarte en 6 (parts égales), cela revient à trouver l'emplacement sur sa circonférence des 6 points à
partir desquels, en joignant le centre, j'obtiens le résultat désiré. Si la circonférence d'un cercle est égale à 2 , on
cherche les points répartis "tous les
, soit 
 ".
[Cela revient aussi à chercher les 6 points correspondant à un angle valant 1/6 de la circonférence, soit 360°/6 = 60°]
Pour couper notre tarte, nous allons donc chercher le point égal à ½ sur l'axe des cosinus ; puis, selon notre
cercle trigonométrique, élever la perpendiculaire qui nous donnera le point de la circonférence égal à 
 .
Voici notre tarte : Coupons-la en 2 parts égales : Marquons le centre :
Nous voilà maintenant avec Repérons les "milieux des côtés" Elevons les perpendiculaires:
un cercle trigonométrique ! (Cos = ½) (points de la circonférence égaux à 
)
Il ne reste plus qu'à couper à partir
des points obtenus sur la
circonférence, en passant par le
centre, pour partager cette tarte en 6
parts égales !!!
Cela marche aussi avec le 4/4, la
forêt noire, la brioche..., du moment
que la pâtisserie est de forme
circulaire.

Enfin,
Rappelons quelques égalités, toujours "autour" du triangle rectangle :
AB + AC > BC
AB² + AC² = BC²
Cos(x) = 
 =  Sin(x)=   =   Tg(x) =   =   = 
Même triangle, mais l'autre angle :
Attention !
Les égalités persistent, mais les côtés n'ont plus la même place relative par rapport à l'angle étudié.
Cos(y) = 
 =   Sin(y)=   =   Tg(y) =   =   = 
D'où la formule mnémotechnique :
Cos = 
 Sin =    tg = 
Cah Soh Toa = "Casse-toi !"
D'autres formules :
Cotg = 
 =    ou tg-1
[Cos(x)]² + [Sin(x)]² = 1 voir Pythagore !
Cos(x)=Cos(-x) Sin(-x)= - Sin(x) Tg(-x) = - Tg(x) Cotg(-x) = - cotg (x) voir cercle trigonométrique
Et puis plein d'autres à découvrir par ailleurs
(en particulier le théorème d'Al-Kashi, appelé également théorème de Pythagore généralisé)...
Côté adjacent
(le côté de l'angle autre que l'hypoténuse)
Côté opposé
x
Hypoténuse
(le plus grand côté du triangle rectangle)
A
B
C
B
y
Hypoténuse
(le plus grand côté du triangle rectangle)
Côté opposé
Côté adjacent
(le côté de l'angle autre
que l'hypoténuse)
A
C