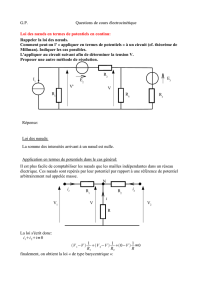
Comment trouver l`état électrique d`un circuit ?

Comment trouver l’état électri
q
ue d’un circuit ? ORGANIGRAMME
élec 2/2
JN Beury
Simplifier le circuit
(Association série, parallèle de résistances, transformation Thévenin, Norton)
circuit série
Diviseur de tension Diviseur de courant Compter le nombre de noeuds
nombre de nœuds ≥ 2
Montage avec un amplificateur opérationnel ?
Loi des mailles
Choisir une grandeur commune
au circuit série (exemple i).
Chercher les potentiels des (n-1) nœuds indépendants
1ère possibilité souvent très rapide :
On cherche les potentiels des (n – 1) nœuds
indépendants. Écrire (n-1) fois la loi des nœuds en
termes de potentiels ou le théorème de Millman.
Remarque importante : si entre deux nœuds, on a
une fem : une des équations s’écrit : VA – VB = e.
2ème possibilité souvent utilisée pour les régimes
transitoires (modélisation d’un câble coaxial) :
Écrire les équations fondamentales de
l’électrocinétique : loi des mailles et loi des nœuds.
pas d’AO
un ou plusieurs AO
ÉQUATIONS À ÉCRIRE : 1) et 2)
1) écrire le théorème de Millman (ou la loi des nœuds en termes de potentiels si ce
n’est pas possible) à tous les nœuds sauf à la masse et à la sortie de l’AO.
2) équation de fonctionnement de l’AO. Par exemple
• 0
ε
=
AO idéal en régime linéaire
• Ssat
VV
=
en saturation positive
• 0
d
d
S
S
VV
t
τ
µε += modèle de l’AO du 1er ordre en régime linéaire
(
ce modèle serait ra
pp
elé dans un exercice
)
En déduire les autres grandeurs électriques du circuit : intensité, tension…
Méthode pour trouver uDE = VD – VE avec D et E points quelconques :
a) penser au diviseur de tension
b) cas particulier où A et B sont des nœuds et A, D, E et B sur la même branche :
1. calculer l’intensité dans la branche AB.
2. en déduire immédiate
m
ent la tension uD
E
.
Le théorème de Thévenin ou de Norton
permet de réduire le nombre de nœuds.

Comment aborder un
p
roblème d’électrocinéti
q
ue ? ORGANIGRAMME
élec 1/2
JN Beury
Quel est le régime étudié ?
Régime transitoire Régime continu
1) Il faut trouver l’équation différentielle :
utiliser les méthodes vues dans
l’ORGANIGRAMME page 2 en dérivant
éventuellement une des équations (loi des
nœuds ou loi des mailles par exemple).
Ne pas utiliser les impédances et amplitudes
complexes.
2) Résoudre l’équation différentielles en 4
étapes : régime libre, régime forcé, somme des
deux et conditions initiales.
On obtient alors le régime transitoire.
Régime sinusoïdal forcé
Utiliser les méthodes vues dans
l’ORGANIGRAMME page 2.
1) Utiliser les amplitudes et impédances complexes.
Voir ORGANIGRAMME page 2 pour en déduire la fonction de
transfert et le diagramme de Bode.
2) La calcul de l’impédance d’entrée et de sortie se fait en utilisant
les méthodes vues dans l’ORGANIGRAMME page 2
3) Pour étudier la réponse à un signal créneau, utiliser la
décomposition en série de Fourier et le théorème de superposition.
(cas particulier du
régime sinusoïdal
forcé avec f = 0)
stabilité du montage :
1) en physique : degré du dénominateur ≥ degré du
numérateur de la fonction de transfert.
2) en physique : pour les systèmes du 1er et 2ème
ordre, vérifier que les coefficients de l’équation
homogène sont de même signe.
Comment trouver l’équation différentielle ?
Lire l’énoncé du problème
Cette méthode systématique
est à connaître parfaitement.
Cette méthode ne peut être utilisée que si l’énoncé le demande
explicitement. Exemples de cas concrets de rédaction :
1) 1ère question : calculer la fonction de transfert. 2ème question :
en déduire l’équation différentielle.
2) 1ère question : calculer la fonction de transfert. 2ème question :
étudier la stabilité du système.
obtention directe de
l’équation différentielle
équation différentielle déduite
de la fonction de transfert