Les fractions

Cours Fractions Page 1 / 9
CH VI) Fractions
I) Représentation d’une fraction :
- Le cercle ci dessous est partagé en 4, hachurer 1 des 4 parties.
On écrit
4
1 du cercle est hachuré.
- Le cercle suivant est partagé en 8, hachurer 2 des 8 parties.
On écrit
8
du cercle est hachuré.
- Hachurer 4 des 11 cases du dessin suivant.
On écrit de la figure est hachuré.
- Indiquer la fraction représentant le nombre de tournevis par rapport à l’ensemble des
outils.
On écrit des outils sont des tournevis.

Cours Fractions Page 2 / 9
Une fraction est notée sous la forme d’un quotient de 2 nombres entiers. Ces deux
nombres sont séparés par un trait appelé barre de fraction.
Le nombre de la partie supérieure de la fraction est le numérateur. Le nombre de la
partie inférieure de la fraction est le dénominateur.
Numérateur
Dénominateur
2
1 se lit un demi.
2
3 se lit trois demis.
3
1 se lit un tiers.
3
4 se lit quatre tiers.
4
1 se lit un quart.
J Toutes les fractions différentes de demi, tiers ou quart se lisent avec le nombre
suivi de ième.
Exemples :
5
3 trois cinquièmes .
21
5 cinq vingt et unièmes.
7
13 treize septièmes.
J On peut écrire une fraction avec une barre oblique
9
4 = 4/9 .
II) Valeur décimale d’une fraction :
Une fraction a pour valeur décimale la valeur obtenue en divisant le numérateur par le
dénominateur. Cette valeur peut être exacte ou approchée.
2
1 = 0, 5 0,5 est la valeur décimale exacte de
2
1.
3
1
≅
0,33 0,33 est la valeur décimale approchée de
3
1.
III) Fractions équivalentes :
Activité : Écrire sous chaque dessin une fraction correspondant à la partie grisée.

Cours Fractions Page 3 / 9
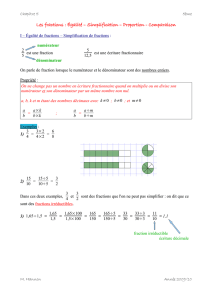
Pour chacune des fractions ci-dessus, calculer sa valeur décimale.
Que peut-on dire pour certaines d’entre elles ?
Les fractions et sont équivalentes, de même que pour et .
Pour les fractions
6
4 et
3
2 calculer : 4 x 3 = 6 x 2 =
Deux fractions
b
a et
d
c sont équivalentes si a x d = b x c.

Cours Fractions Page 4 / 9
IV) Différentes écritures d’une fraction :
On obtient une fraction équivalente à une fraction donnée en multipliant ou en divisant
quand c’est possible numérateur et dénominateur par un même nombre.
x 3
: 2 x 6
6
4=
3
2=
18
12
: 2 x 6
x 3
Exercice : Compléter la « chaîne » de fractions suivante.
3
2=
6
=
9
=12 =24 =
15
=14
V) Simplification d’une fraction :
1) Définition :
Pour simplifier une fraction, on divise le numérateur et le dénominateur par un même
nombre entier. Lorsque les deux termes n’ont plus de diviseur commun, on dit que la
fraction est irréductible.
Exemple :
12
20 =
6
10 =
3
5et
3
5 est une fraction irréductible.
Exercice : Écrire sous forme de fraction irréductible.
24
30 =
120
80 =
72
48 =
750
2501 =
450
375 =
420
660 =

Cours Fractions Page 5 / 9
2) Quelques règles de divisibilité :
J Il n’est pas évident de déterminer le même nombre qui divise le numérateur et le
dénominateur sans utiliser de calculatrice. Observez les règles de divisibilité suivantes,
elles devraient beaucoup vous aider.
Divisibilité par :
à 2 : Un nombre est divisible par 2 lorsqu’il est pair (Rappel : un nombre est pair lorsqu’il
se termine par 0 ; 2 ; 4 ; 6 ou 8)
à 3 : Un nombre est divisible par 3 lorsque la somme des chiffres qui le composent est
un multiple de 3. ( Rappel : un multiple d’un nombre est son résultat dans la table de
multiplication.)
Ex : 2 283 à 2 + 2 + 8 + 3 = 15 à 1 + 5 = 6 6 étant un multiple de 3, 2 283 est divisible
par 3.
à 4 : Un nombre est divisible par 4 lorsqu’il est deux fois divisible par 2.
Noter que c’est de cette façon que l’on détermine si une année est bissextile. 2004 sera
une année bissextile puisque 2004 / 2 = 1002 et 1002 / 2 = 501.
à 5 : Un nombre est divisible par 5 lorsqu’il se termine par 0 ou 5.
à 9 : Un nombre est divisible par 9 lorsque la somme des chiffres qui le composent est
un multiple de 9.
à 10 : Un nombre est divisible par 10 lorsqu’il se termine par 0.
à 11 : Un nombre est divisible par 11 lorsque la différence entre la somme des chiffres
pairs et la somme des chiffres impairs ( ou inversement) est égale à 0 ou à un multiple de
11.
Chiffres de rang pair 7 + 7 = 14
Ex : 7 172 14 - 3 = 11
Chiffres de rang impair 2 + 1 = 3
J 6 ; 8 ; 12 etc… correspondent à des combinaison de nombres divisibles.
6 si divisible par 2 et par 3 2 x 3 = 6
8 si divisible par2, puis encore par 2 et encore par 2 8 = 2 x 2 x2 etc…
Exercice : Compléter le tableau en indiquant par une croix si le nombre est divisible.