Chap 9 (phys): Travail et énergie mécanique. Objectif : Etre capable

Chap 9 (phys): Travail et énergie mécanique.
Objectif :
I)
Etre capable de calculer le travail d’une force
Définir les forces conservatives ou non.
Savoir utiliser le théorème de l’énergie mécanique
Travail d’une force
1) Transfert d’énergie
Energie biochimique de Mr
Energie cinétique
Def : Le travail mécanique d’une force est l’énergie fourni au système qui subit la force lorsqu’il se
déplace.
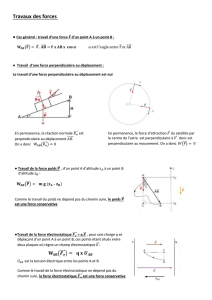
2) Travail d’un force constante :
Def : Le travail d’une force constante exercé sur un objet allant du point A au point B s’écrit
WAB (F-->) =F->.AB->
=F x AB x cos α où α= (F ; AB)
Joules (J)



Lorsque l’angle α vaut entre 0 et 90°, cos α est positif, le travail de la force sera donc positif
on parle de travail moteur.
Si 90<α<180, cos négatif donc W négatif, on dit qu’il est résistant.
Si α=90° , cos =0 , W=0


3) Forces conservatives ou non :
Def : Une force est conservative si son travail entre 2 points A et B quelque conque ne
dépendent pas de la trajectoire suivie entre ces 2 points.
Toutes les forces constantes sont conservatives : Le poids P->, force électrique Fe->, force
rappel ressort Fr->.
Les forces de frottement ou la force de tension d’un fil sont des forces non conservatives.
II ) Travaux de quelques forces ( DEMO A CONNAITRE )
1) Travail du poids
W(P-> )= P->.AB->
=P x AB x cos α
=m x g x AB x cos α
=m x g x AB x AC/ AB
=m x g x AC
= m x g x (zA-zB)
Le travail du poids d’un objet de masse m entre le point A, altitude zA et le point B à l’altitude zB
s’écrit :
W(P->)(J)= m (kg) x g(N.kg-1)x(zA-zB) = m x g x h
Rq : lorsqu’on passe d’une altitude supérieur à une altitude inférieur, si zA > zB , le travail du poids est
positif, le travail est moteur
Dans le cadre ou on passe d’une altitude inférieur à une altitude supérieur, le travail du poids sera
négative, la force du poids sera résistante.
Si on reste à la même altitude, zA=zb , W = 0
Appli : un panier de basket est situé à une hauteur H = 3.05m, le ballon de masse 650g est lancé par
un joueur à une hauteur h = 2.20m du sol. Calculer le travail du poids entre le point de lancer et le
panier.
W = m x g x (h-H) = 0.65*9.81*-0.85 = -5.42 J –> travail résistant.
2) Travail de la force électrique Fe->
Démonstration à connaitre :
WA->B(F->e)
= Fe . AB->
= Fe -> . (AC-> + CB->)
= Fe -> . AC-> + Fe-> . CB->
WA->B(Fe->)
=0
= Fe x AC x cos α
= Fe x AC
= q x E x AC
= q x UAC
(=UAB )
Le travail de la force électrique Fe-> Sur une particule de charge q qui va de A vers B dans un champs
uniforme E vaut
WA->B(Fe->) (J)= q (coulombs) x UAB (Volts)
4) Travail de force de frottements :
Monte
A
F->frottement
B
Le travail de F->frottement :
W (F) = Ff-> . AB->
= Ff x AB x cosα
= -Ff x AB < 0
travail résistant  force non conservatrice
L’énergie est transférée sous forme thermique donc chaleur, elle est perdue par le système.
III ) Conservation de l’énergie mécanique :
1) Energie potentielle d’une force conservative :
On définit la variation d’énergie potentielle comme l’opposé du travail de la force conservative.
ΔE Ppesanteur A-> B = - WA->B (P->)
EPp(B) - EPp(A) = - m x g x (zA-zB)
= m x g x (zB-zA)
EPp(B) = m x g x zB
EPp(A) = m x g x zA
Epotentielle pesanteur = m x g x z +cste
Epotentielle électrique = q x V + cste
2) Définition de l’énergie mécanique Em
Def : L’énergie mécanique Em d’un système soumit à des forces conservatives est la
somme de son énergie cinétique Ec et de ses énergie potentielle Ep.
Em = Ec + Epp + Epe + … (tout en joule)
Où Ec = ½ x m x v2
Où Epp = mgz + cste
3) Transferts énergétiques
Théorème de l’énergie mécanique :
La variation d’énergie mécanique sur un trajet allant de A vers B est égal à la somme des travaux des
forces non-conservatives. Ce qui veut dire :
ΔEm
= Em(B) – Em(A)
= ƩW (F->non-conservatives)
Rq : ΔEm = ΔEc + ƩΔEp
Si un système ne subit pas de force non-conservatives, la variation d’énergie est nul ΔEm= 0, il y a
transfert d’énergie entre l’énergie cinétique et l’énergie potentielle
Forces conservatrices : P->
Forces non conservatives : f-> (frottement), T->(tension fil), R-> (réaction)
ΔEm = ƩW (F->non-conservatives)
= W (f->) + W(T->) +W(R->) <= =0
<0
>0
= ΔEc +ΔEpp
=0
>0
A vitesse v = cste  ΔEc = Ec(B) – Ec(A)= 0