Correction de l`exercice 2 p 269 Réponses justes : a c a Correction

Correction de l'exercice 2 p 269
Réponses justes :
1. a
2. c
3. a
Correction de l'exercice 3 p 269
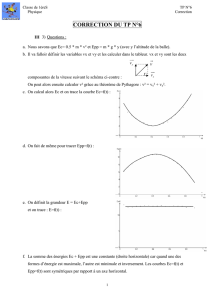
Une chronophotographie est réalisée en superposant des clichés pris à intervalles de temps réguliers d'un objet en
mouvement. Entre deux positions de la bille, il s'est donc écoulé des durées égales.
Comme la bille parcourt des distances de plus en plus grandes en des durées égales, on peut dire que la vitesse de la
bille augmente au cours de sa chute.
L'énergie cinétique variant comme la vitesse au carré de la bille, on peut donc en déduire que l'énergie cinétique de
la bille augmente au fur et à mesure de la chute.
Correction de l'exercice 5 p 269
1. Par définition, 
 avec Ec en J, m en kg et v en m/s.
D'où 
L'énergie cinétique communiquée au poids au moment du lancer est de 2,0 × 102 J.
2. Au moment de l'impact avec le sol, cette énergie est en partie transformée en énergie thermique (qui va être
responsable d'une légère élévation de température du poids mais aussi du sol du fait des frottements entre le
poids et le sol).
Par ailleurs, cette énergie mécanique du poids va aussi certainement être en partie communiquée sous forme
d'énergie mécanique au sable ou à la terre car une partie de la matière va être sans doute mise en mouvement
sous l'effet du choc.
Correction de l'exercice 10 p 269
Réponses justes :
1. c. : on ne peut pas répondre. En effet, tout dépend de l'origine des énergies potentielles que l'on choisit.
2. c. : Si un objet tombe de y mètres, alors il perd une énergie potentielle de pesanteur de mgy avec m en kg et g en
N/kg.
Par conséquent, un objet qui perd 1 J d'énergie potentielle au cours d'une chute est tombé d'une hauteur y =
1/(mg) ≈ 1/(0,1×10) = 1 m
NB : en réalité, la formulation de la question est un peu maladroite car l'énergie mécanique est toujours définie à
une constante près. Il aurait été plus juste d'écrire :
"1 Joule est environ l'énergie cinétique gagnée au cours de sa chute par un objet de 100 g qui tombe de : "
3. a. : Une énergie potentielle de pesanteur. Si on estime que la personne se laisse tomber sans vitesse initiale, son
énergie cinétique est en effet nulle à l'instant où elle commence à tomber.

Correction de l'exercice 14 p 269
1. Par définition, l'énergie potentielle d'un objet de masse m vaut Epp (h) = mgh + K où :
 m est en kg,
 g est l'intensité de la pesanteur en N/kg,
 h est l'altitude à laquelle se trouve l'objet
 et K est une constante en J, que l'on peut choisir arbitrairement,
car seules les différences d'énergies potentielles ont un sens
physique.
Pour clarifier le problème, on définit un axe vertical dont l'origine est situé
au niveau du sol (voir ci-contre).
Suivant ce schéma : h = y.
a. Si Epp = 0 J au niveau du sol,
alors Epp (0) = mg×0 + K = 0
d'où K = 0 J
Dans ce cas, on obtient que l'énergie potentielle de Taig Kris lorsqu'il est au premier étage est de
Epp = mgy + 0
Epp = 90 × 9,81 × 57,63
Epp = 5,1 × 104 J
b. Si Epp = 0 J au niveau du premier étage, alors l'énergie potentielle de Taig Kris lorsqu'il est au premier
étage est de 0 J.
c. Si Epp = 0 J au niveau du deuxième étage,
alors Epp (115,73 m) = m × g ×115,73 + K = 0 J
On en déduit que K = - 90 × 9,81 ×115,73 J
On peut alors calculer l'énergie potentielle de Taig Kris situé au premier étage :
Epp = mgy + K
Epp = 90 × 9,81 × (57,63 - 115,73)
Epp = - 5,1 × 104 J
d. Si Epp = 0 J au niveau du troisième étage,
alors Epp (276,13 m) = m × g × 276,13 + K = 0 J
On en déduit que K = - 90 × 9,81 × 276,13 J
On peut alors calculer l'énergie potentielle de Taig Kris situé au premier étage :
Epp = mgy + K
Epp = 90 × 9,81 × (57,63 - 276,13)
Epp = - 1,9 × 105 J
2. On dit que l'énergie potentielle de pesanteur d'un système est une grandeur algébrique car c'est une grandeur
qui peut prendre des valeurs négatives si le système est placé à une altitude plus basse que celle à laquelle on a
fixé l'origine des énergies potentielles de pesanteur.