Chapitre 3: Méthodes d`estimation et tests classiques sur un

Chapitre 3: Méthodes d’estimation et tests classiques
sur un échantillon gaussien
Léonard Gallardo∗
1 Etude des échantillons gaussiens
On rappelle qu’un n-échantillon d’une loi Fest un n-uplet (X1, . . . , Xn)de variables
aléatoires i.i.d. de même loi Fet définies sur un certain espace probabilisé (Ω,F,P)qu’on
ne précisera pas forcément. Il est commode de considérer ce n-échantillon comme le vecteur
aléatoire X:= (X1, . . . , Xn)de Rndont les composantes sont les Xi; c’est ce que nous ferons
toujours par la suite.
1.1 La loi du χ2à n degrés de liberté
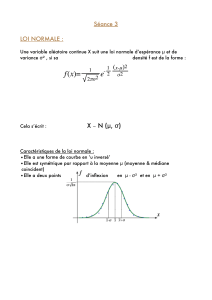
On rappelle qu’une variable aléatoire Xsuit la loi Gamma de paramètres α > 0et b > 0
(notée Γ(α, b)) si elle a une densité de probabilité donnée par :
(1) fα,b(x) = bα
Γ(α)xα−1e−bx1[0,∞[(x).
Proposition 1.1 : La fonction caractéristique φXd’une variable aléatoire Xde loi Γ(α, b)
est de la forme
(2) φX(t) = 1−it
b−α
.
démonstration :φX(t) = bα
Γ(α)Z∞
0
eitxxα−1e−bxdx. D’où en développant eitx en série en-
tière :
φX(t) = bα
Γ(α)
∞
X
n=0
(it)n
n!Z∞
0
xn+α−1e−bxdx
=∞
X
n=0
(it)n
n!
bα
Γ(α)
1
bn+αZ∞
0
xn+α−1e−xdx
=∞
X
n=0
Γ(n+α)
n!Γ(α)it bn
+∞
X
n=0
(α+n−1)(α+n−2) ···α
n!it bn
=1−it
b−α
.
∗cours de Statistiques, Master 1, Université de Tours, année 2007-2008, Laboratoire de Mathématiques
et Physique Théorique-UMR 6083, Parc de Grandmont, 37200 TOURS, FRANCE. email : gallardo@univ-
tours.fr
1

Corollaire 1.2 : Une variable aléatoire Xde loi Γ(α, b)a des moments de tous les ordres
et en particulier
(3) E(X) = α
b,E(X2) = α(α+ 1) b2, V ar(X) = α b2
démonstration :φX(t)est indéfiniment dérivable donc Xa des moments de tous les ordres.
En dérivant φXdeux fois, on obtient
φ0
X(t) = iα
b1−it b−α−1
, φ00
X(t) = i2α(α+ 1)
b21−it b−α−2
D’où le résultat en faisant t= 0.
Corollaire 1.3 (additivité des lois Gamma) : Soient X1, . . . , Xndes variables aléatoires
indépendantes de lois respectives Γ(α1, b),...,Γ(αn, b). Alors la variable aléatoire X1+···+
Xnsuit la loi Γ(α1+··· +αn, b).
démonstration : D’après (2) est l’indépendance des Xi, la fonction caractéristique de la
variable aléatoire X1+··· +Xnvaut :
φX1+···+Xn(t) =
n
Y
k=1 1−it
b−αk
=1−it
b−(α1+···+αn)
.
C’est la fonction caractéristique d’une loi Γ(α1+··· +αn, b).
Corollaire 1.4 : Soit (X1, . . . , Xn)un n-échantillon de la loi normale N(0,1). Alors la
variable aléatoire χ2
n=X2 1+··· +X2 nsuit la loi Γ(n
2,1 2). Elle a pour densité
(4) fχ2
n(x) = 2−n/2
Γ(n
2)xn
2−1e−1 2x1[0,∞[(x).
et elle est telle que
(5) E(χ2
n) = net V ar(χ2 n) = 2n.
démonstration : Il suffit de prouver ce résultat pour n= 1 puis d’appliquer le corollaire
1.3. Soit Xune variable aléatoire N(0,1). La fonction caractéristique de X2est égale à
φX2(t) = E(eitX2) = 1
√2πZ∞
−∞
eitx2e−x2/2dx
=1
√2πZ∞
−∞
e−1
2x2(1−2it)dx = (1 −2it)−1/2.
On reconnait l’expression de la fonction caractéristique de la loi Γ(1
2,1 2). d’où le résultat. 
Définition 1.5 : La loi de la variable aléatoire du corollaire précédent s’appelle loi du χ2
àndegrés de liberté.
2

Comme consèquence du corollaire 1.3, on a l’additivité des lois pour des variables du chi-deux
indépendantes :
Corollaire 1.6 : Si (Xi)1≤i≤kest une famille finie de variables aléatoires indépendantes
telle que pour tout i,Xisuit une loi χ2
ni, alors la variable aléatoire Pk
i=1 Xisuit la loi χ2
noù
n=Pk
i=1 ni.
Remarque : Pour le calcul du corollaire 1.4, on a utilisé le fait que pour tout m∈Ret tout
z∈Ctel que Re(z)>0, on a
(6) 1
√2πZ∞
−∞
e−1
2(x−m z)2
dx =z.
En effet la formule est vraie pour z > 0et comme le premier membre de (6) est une fonction
holomorphe de la variable zdans le demi-plan Re(z)>0, le résultat en découle par prolon-
gement analytique.
Remarque et Notation : Soit X= (X1, . . . , Xn)un n-échantillon de la loi normale N(0,1)
et soit σ > 0. Alors σX = (σX1, . . . , σXn)est un n-échantillon de la loi normale N(0, σ2).
La variable aléatoire ||σX||2=σ2(X2
1+···+X2 n)et sa loi seront alors notés σ2χ2 n. Attention,
quand on parlera de la loi σ2χ2
n, il faudra se souvenir que c’est la variable aléatoire χ2 nqui
est multipliée par σ2et non sa fonction de répartition !
1.2 Transformation orthogonale d’un n-échantillon gaussien. Théo-
rème de Cochran
Le but de ce paragraphe est de mettre en évidence une propriété remarquable des n-
échantillons gaussiens : la conservation de leur nature par changement de base orthonormale
ou par transformation orthogonale de Rn. Cette propriété géomètrique est à la base des mé-
thodes statistiques d’estimation et de tests liées aux lois gaussiennes. Tout d’abord il convient
de savoir reconnaître facilement un n-échantillons gaussien. L’outil théorique "infaillible"
qui permet de voir si un vecteur (resp. une loi) est gaussien (resp. gaussienne) et qui permet
aussi de dire si ses composantes (resp. ses marginales) sont indépendantes est la fonction
caractéristique :
Théorème 1.7 :X= (X1, . . . , Xn)un n-échantillon de la loi normale N(0, σ2)si et seule-
ment si la fonction caractéristique φXde Xest de la forme
(7) φX(t) = exp(−1
2σ2||t||2)t∈Rn,
où ||t|| =pt2
1+··· +t2
nest la norme euclidienne du vecteur t= (t1, . . . , tn).
démonstration : 1) (C.N.) Soit X= (X1, . . . , Xn)un n-échantillon de la loi normale
N(0, σ2)et soit t∈Rn. Grâce à l’indépendance des Xk, on a :
φX(t) = E(ei<t|X>) = E n
Y
k=1
eitkXk!=
n
Y
k=1
E(eitkXk)
=
n
Y
k=1
exp −1
2σ2t2
k= exp −1
2σ2||t||2.
3

2) (C.S.) Si X= (X1, . . . , Xn)est un vecteur aléatoire de fonction de caractéristique φX(t) =
exp(−1
2σ2||t||2)(t= (t1, . . . , tn)∈Rn), alors pout tout k= 1, . . . , n, on a
φXk(tk) = φX(0,...,0, tk,0,...,0) = e−σ2
2t2
k.
Ce qui montre que Xkest de loi N(0, σ2). De plus comme pour tout t∈Rn,φX(t) =
Qn
k=1 φXk(tk), les variables aléatoires Xksont indépendantes. 
Remarque : Si Xest un n-échantillon de la loi normale N(0, σ2), alors pour tout t∈Rn,
la variable aléatoire réelle < t|X > (produit scalaire de tet X) est de loi N(0, σ2||t||2)car
pour u∈R,
(8) φ<t|X>(u) = E(eiu<t|X>) = E(ei<ut|X>) = e−σ2
2||ut||2=e−σ2||t||2 2u2
est la fonction caractéristique de la loi N(0, σ2||t||2).
Théorème 1.8 (de Cochran) : Soit X= (X1, . . . , Xn)un n-échantillon de la loi normale
N(0, σ2). Alors :
1) les composantes de Xdans toute base orthonormale de Rn, forment aussi un n-échantillon
de la loi N(0, σ2).
2) Le transformé du vecteur Xpar une transformation orthogonale de Rn, est toujours un
n-échantillon de la loi N(0, σ2).
3) Soit E1⊕···⊕Epune décomposition de Rnen psous espaces vectoriels deux à deux ortho-
gonaux et de dimensions respectives r1, . . . , rp. Alors les vecteurs aléatoires XE1, . . . , XEppro-
jections orthogonales respectives de Xsur E1, . . . , Ep, sont indépendants. De plus les variables
aléatoires ||XE1||2,...,||XEp||2sont indépendantes et de lois respectives σ2χ2
r1, . . . , σ2χ2 rp.
démonstration : Soit v1, . . . , vnune base orthonormale de Rn. On a évidemment X=
Pn
k=1 < X|vk> vk. Le vecteur X0= (< X|v1>, . . . , < X|vn>)a pour fonction caractéris-
tique
φX0(t) = E(eiPn
k=1 tk<X|vk>) = Eei<X|Pn k=1 tkvk>
=φX(
n
X
k=1
tkvk) = exp −1
2σ2||
n
X
k=1
tkvk||2= exp −1
2σ2||t||2,
d’après le théorème 1.5 et en utilisant le fait que (vk)est une base orthonormale pour affir-
mer que ||Pn
k=1 tkvk||2=Pn k=1 t2
k=||t||2. Du théorème 1.5, on obtient alors que X0est un
n-échantillon de la loi N(0, σ2).
2) Cette assertion n’est qu’une formulation équivalente de 1). En effet soit Aune matrice
orthogonale n×n. Par définition ses vecteurs lignes v1, . . . , vn, forment une base orthonor-
male de Rn. Le vecteur AX transformé de Xpar l’action de la matrice Aest le vecteur de
Rnde coordonnées < X|v1>, . . . , < X|vn>(dans la base canonique) donc c’est encore un
n-échantillon de la loi N(0, σ2)d’après le 1). 
3) Choisissons dans chaque sous espace Ejune base orthonormale {vj,1, . . . , vj,rj}et munis-
sons Rnde la base orthonormale Bobtenue en réunissant toutes ces bases. La projection
orthogonale XEjdu vecteur aléatoire Xsur Ej, est alors égale à
XEj=
rj
X
k=1
< X|vj,k > vj,k
4

Les vecteurs aléatoires XEjsont clairement indépendants puisque leurs composantes <
X|vr,s >dans la base Bsont des variables aléatoires indépendantes d’après le 1). Il en
résulte aussi que les variables ||XE1||2,...,||XEp||2sont indépendantes. D’autre part, d’après
le théorème de Pythagore, on a
||XEj||2=
rj
X
k=1 |< X|vj,k >|2.
Le corollaire 1.4 et la remarque qui suit, montrent alors que ||XEj||2suit la loi σ2χ2
rj.
2 Statistiques fondamentales d’un échantillon gaussien
Dans le langage des statisticiens, le "terme statistique " lorsqu’il est associé à échantillon",
est un synonyme de variable aléatoire liée à l’échantillon . Ainsi par exemple la moyenne et
la variance empirique sont les statistiques importantes d’un échantillon.
Définition 2.1 : Soit X= (X1, . . . , Xn)un n-échantillon de la loi N(m, σ2). Alors les
statistiques (variables aléatoires)
¯
X=1
n
n
X
i=1
Xi,(9)
S2=1
n−1
n
X
i=1
(Xi−¯ X)2,(10)
s’appellent respectivement la moyenne et la variance empirique du n-échantillon X.
Remarque 1 : Pour l’échantillon centré ˜ X= (X1−m,...,Xn−m)on a ¯
˜
X=¯ X−met
˜
S2=S2. On retiendra cette invariance du S2par centrage de l’échantillon.
Remarque 2 :¯ Xet S2sont des "estimateurs" respectivement des paramètres met σ2
de la loi de l’échantillon, d’où la terminologie adoptée. Précisons qu’on appelle estimateur
d’un certain paramètre lié à une loi, une statistique (variable aléatoire) qui converge (en un
certain sens1) vers la valeur du paramètre lorsque la taille nde l’échantillon tend vers l’infini.
En effet, on a ici
¯
X=1
n
n
X
i=1
Xi→m p.s. (n→ ∞),
d’après la loi forte des grands nombres (voir le cours de Probabilités). De même, puisqu’on
peut écrire S2=1
n−1Pn
i=1(Xi−¯
X)2=1
n−1Pn
i=1 X2
i−n
n−1(¯
X)2, on voit que
S2→E(X2
1−(E(X1))2=σ2p.s. (n→ ∞).
toujours d’après la loi forte des grands nombres.
Théorème 2.2 : Si X= (X1, . . . , Xn)est un n-échantillon de la loi N(m, σ2), les variables
aléatoires ¯ Xet S2définies en (9) et (10) sont indépendantes. De plus
1par exemple pour la convergence p.s. ou la convergence L2, etc...
5