Thème : Electricité Fiche 6 : Oscillations libres du circuit

© Tous droits réservés Studyrama 2006
PHYSIQUE Série S
Nº : 36006
Fiche téléchargée sur www.studyrama.com 1
Fiche Cours
Plan de la che
1. Dénitions
2. Règles
3. Méthodologie
I - Dénitions
• Circuit RLC série : circuit constitué de l’association en série d’une bobine (d’inductance L et de résistance r), d’un condensateur
(de capacité C) et d’un conducteur ohmique (de résistance R).
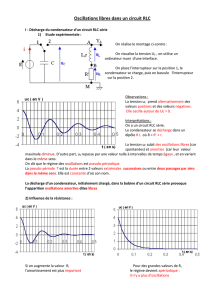
• Régime libre d’un circuit RLC série : régime pour lequel le circuit ne subit aucun apport d’énergie après l’instant initial. Cette
situation correspond à la décharge d’un condensateur dans un dipôle RL.
• Régime pseudo-périodique d’un circuit RLC série : régime pour lequel la tension
C
u
aux bornes du condensateur présente
des oscillations amorties (oscillations dont l’amplitude décroît au cours du temps).
• Amplitude d’une grandeur : valeur absolue de la grandeur concernée.
• Régime apériodique d’un circuit RLC série : régime pour lequel la tension
C
u
aux bornes du condensateur ne présente
pas d’oscillations et tend vers la valeur nulle. Le régime apériodique critique correspond à la situation où la tension
C
u
tend le
plus rapidement vers la valeur nulle.
• Pseudo période : intervalle de temps entre deux maxima (ou deux minima) successifs d’un régime pseudo-périodique.
• Régime périodique d’un circuit LC : régime pour lequel les grandeurs électriques suivent des oscillations sinusoïdales, de
période
0
T
appelée période propre du circuit LC. Le circuit LC est un circuit idéal où la valeur de la résistance totale du circuit
est nulle :
TOTALE
R
= r + R = 0.
• Période propre d’un circuit LC :
( ) 2/1
0CL2T ××π=
.
II - Règle
Propriétés
• Propriété n°1
Dans le régime libre, l’équation différentielle de la tension
C
u
aux bornes du condensateur s’établit de la manière suivante :
0uuu CLR =++
(application de la loi d’additivité des tensions) avec :
iRuR=
;
( )[ ]
td/idLiruL×+=
;
C/quC=
.
Compte tenu que : i = dq / dt, on en déduit :
( )
td/udCi C ×=
. Ce qui conduit à :
( )[ ] ( )[ ] ( )[ ] 0utd/udCLtd/udCrtd/udCR C
2
C
2
CC =+×+×+×
.
Soit :
( ) ( )[ ] ( ){ } ( )[ ] 0CL/utd/udL/rRtd/ud CC
2
C
2=+×++
.
Le terme
( )[ ] ( ){ }
td/udL/rR C ×+
est le terme d’amortissement.
Suivant la valeur de (R + r), on observe :
- un régime périodique si R + r = 0 ;
- un régime pseudo-périodique si R + r ≥ 0 ;
- un régime apériodique si R + r > 0.
Thème : Electricité
Fiche 6 : Oscillations libres du circuit RLC série

© Tous droits réservés Studyrama 2006
PHYSIQUE Série S
Nº : 36006
Fiche téléchargée sur www.studyrama.com 2
Fiche Cours
• Propriété n°2
Dans le régime périodique (circuit LC), l’équation différentielle de
C
u
s’écrit :
( ) ( )[ ] 0CL/utd/ud C
2
C
2=+
Compte tenu que q = C
C
u
, on établit l’équation différentielle de q :
( ) ( )[ ] ( )[ ] 0CL/qtd/qdC/1 222 =+×
.
Soit :
( ) ( )
[ ] 0CL/qtd/qd
22
=+
La solution générale de ces équations différentielles correspond à la situation où la fonction est égale à sa dérivée seconde. La
fonction cosinus présente cette propriété.
Donc :
)t(uC
= A cos {[(2π × t) /
0
T
] + φ}
et q(t) = B cos {[(2π × t) /
0
T
] + φ
A est l’amplitude des oscillations de
C
u
.
B est l’amplitude des oscillations de q.
[(2π × t ) /
0
T
] + φ est la phase des oscillations de
C
u
et q.
A, B et φ sont des constantes qui sont déterminées à partir des conditions du circuit.
Les grandeurs
C
u
et q sont continues, ce qui impose les conditions initiales du circuit LC :
0C U)0(u =
et q(0) = C
0
u
Avant la fermeture, l’intensité dans le circuit est nulle. La présence d’une bobine garantit la continuité de l’intensité : i(0) = 0
i(t) = C (
C
ud
/ dt) = - (2π A /
0
T
) sin {([ 2π × t) /
0
T
] + φ }.
Or : i(0) = - 2 π A /
0
T
sin φ = 0, ce qui conduit à φ = 0 ou φ = π.
)0(uC
= A cos φ =
0
U
conduisant à φ = 0.
Soit :
0C U)t(u =
cos [(2π × t) /
0
T
]
q(t) =
0
UC
cos [(2π × t) /
0
T
]
i(t) = - (2π /
0
T
) ×
0
U
× sin [(2π × t) /
0
T
]
=
( )
2/1
0L/CU ×−
× sin [(2π × t) /
0
T
]
Lorsque
)t(uC
est nulle, i(t) est maximale (ou minimale). Inversement, lorsque
)t(uC
est maximale (ou minimale), i(t) est nulle.
• Propriété n°3
Dans un circuit LC, le bilan énergétique traduit des allers-retours d’énergie entre le condensateur et la bobine :
C
E
= (1 / 2) ×
( )
2
C
uC
= (1 / 2) ×
( ) 2
2
0cosUC ×
[(2π × t) /
0
T
]
( ) ( ) ( ) ( ) ( )
[ ]
0
2
2
0
2
0
222
LT/t2sinUT/4CL2/1iL2/1E ×π××π××=×=
.
Or :
( ) 2/1
0CLT =
. Ce qui conduit à :
( ) 1T/4CL 2
0
2=π×
.
L’énergie totale est :
( ) ( ) ( )[ ]
{ } ( )[ ] { }
0
2
0
2
2
0LC T/t2sinT/t2cosUC2/1EEE ×π+×π××=+=
.
Soit : E = (1 / 2) ×
( )
2
0
UC
Il y a un transfert périodique d’énergie entre le condensateur et la bobine. L’énergie totale emmagasinée dans le circuit reste
constante.
• Propriété n°4
Dans le régime pseudo-périodique, les oscillations présentent des amplitudes décroissantes.
La pseudo-période dépend des valeurs de r, L et C mais ne dépend pas des conditions initiales.
Pour des régimes pseudo-périodiques peu amortis, les pseudo-périodes sont quasi identiques.
L’équation différentielle traduisant l’évolution de
C
u
s’écrit :
( ) ( )[ ] ( ) ( )[ ] 0CL/utd/udL/rRtd/ud CC
2
C
2=+×++
.
Compte tenu que i = C ×
( )
td/ud C
et
C
u
= (q / C),
on en déduit : di / dt = C ×
( )
2
C
2td/ud
L’équation différentielle s’écrit alors :
[(1 / C) × (di / dt)] + {[(R + r) / LC] × i} + (q / L) = 0
Soit : [L × (di / dt)] + [(R + r)] i + (q / C) = 0
En multipliant les deux membres par i, on obtient :
[L × i × (di / dt)] + {[(R + r)] ×
2
i
} + [(q / C) × (dq / dt)] = 0
Soit : {L × [d / dt
( )
2/i2
]} + {[(R + r)] ×
2
i
} + {(1 / C) × [d / dt
( )
C/q2
]} = 0

© Tous droits réservés Studyrama 2006
PHYSIQUE Série S
Nº : 36006
Fiche téléchargée sur www.studyrama.com 3
Fiche Cours
D’où : {[(R+ r)] ×
2
i
} + {d / dt [L
2
i
+
( )
C2/q2
]} = 0
Or :
( ) 2
LiL2/1E ×=
et
( ) ( ) C/q2/1E 2
C×=
Soit : (R + r) ×
2
i
+ (dE / dt) = 0
Ce qui conduit à (dE / dt) < 0 : une partie de l’énergie emmagasinée par le condensateur et la bobine est dissipée dans la résistance
(R + r) par effet Joule.
• Propriété n°5
Pour compenser les pertes énergétiques du dipôle RLC série, on envisage de lui associer un dipôle D qui lui restitue à chaque
instant l’énergie qu’il perd.
Le dipôle D se comporte comme une résistance négative, de même valeur absolue que (R + r) et telle que :
D
u
= - (R + r) i.
III - Méthodologie
• La période propre du circuit LC est :
( ) 2/1
0CL2T ××π=
Ce résultat peut se retrouver à partir de l’équation différentielle traduisant l’évolution de
C
u
:
( ) ( )[ ] 0CL/utd/ud C
2
C
2=+
.
Sachant que
( )
[ ]
00C T/t2cosUu ×π=
, on obtient :
( ) ( )[ ]
{ } ( ) ( )[ ]{ } 0T/t2cosCL/UT/t2cosT/2U 000
2
00 =×π×+×π×π×−
.
D’où :
( ) ( )[ ] ( )[ ] ( )[ ]
000
2
00 T/t2cosCL/UT/t2cosT/2U ×π−=×π×π×−
.
Soit par identication :
( ) 2/1
0CL2T ××π=
• La période propre du circuit LC est homogène à un temps
En effet, l’analyse dimensionnelle conduit à : [LC] = [L] × [C]
Or :
L
u
= L × (di / dt) conduit à : [L] = {[U] × T} / I
et
( )
C
u/qC =
conduit à : [C] = {I × T} / [U]
Soit :
[ ]
TCL 2/1 =
: homogène à un temps.