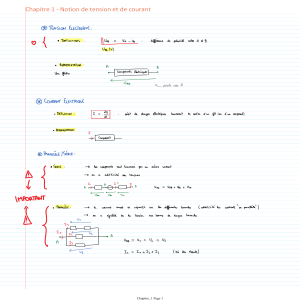
Exercice n°1 : Puissance moyenne. - mpsi

PTSI 1 TD ELECTROCINETIQUE 5 2005/2006
Puissance en régime sinusoïdal forcé.
Exercice n°1 : Puissance moyenne.
Déterminer la puissance moyenne consommée par le groupement (R, L) //(C, r) alimenté
par la tension sinusoïdale u(t) = U
2
cos(t).
Exercice n° 2 : Optimisation du fonctionnement d'un moteur.
EDF fournit une tension efficace U = 220 V la fréquence de 50 Hz.
1. Un particulier branche un appareil de chauffage (non inductif) qui consomme P 1 = 1 kW et un moteur inductif modélisable
par une résistance A et une réactance B) de puissance P 2 = 2 kW et de facteur de puissance cos 2 = 0,5.
Définir les intensités i1, i2 dans les deux dérivations et i dans la ligne d’alimentation et en déduire le facteur de puissance de
l’installation.
2. EDF recommande d’améliorer le facteur de puissance. Pour cela, on adjoint un condensateur en dérivation. Quelle est la
valeur de C qui permet d’obtenir un facteur de puissance égal à 1 ?
Exercice n°3 : Étude énergétique d'un circuit.
Considérons le circuit, alimenté entre A et B par une tension sinusoïdale u, de fréquence
f et de valeur efficace U.
La résistance R est susceptible de varier (résistance réglable). On note P la puissance
moyenne consommée par le circuit.
Données : : U = 220 V, f = 50 Hz, L = 1 H, P est maximale (valeur P M) pour R = 12  ;
d'autre part, pour R = R1 > 12 , le facteur de puissance du circuit est égal à l'unité et P = 800 W.
Calculer numériquement P M, L', Rl, C.
Exercice n°4 : Adaptation d'impédances
On connecte en série deux dipôles DG et D d'impédances ZG et Z. Z et ZG sont des
impédances quelconques qui en notation complexe peuvent être mises sous la forme
XYZj
et
GG
XY
G
Zj
avec j2 = - 1.
1. Démontrer que la puissance électrique moyenne P dissipée dans le dipôle D est maximale
lorsque
G
ZZ
(* signifie complexe conjugué).
2. Que se passe-t-il si
Z
est purement imaginaire ? Que devient l'énergie fournie par la source ?
3. Pour f = 150.106 Hz, déterminer la nature du dipôle DG dans les cas suivants :
3.a. D est une résistance pure de 150  en parallèle avec un condensateur de capacité 100 pF ;
3.b. D est constitué par une résistance pure de 150  en parallèle avec une bobine pure d'inductance 3.10-8 H.
Exercice n°5 : Interprétation énergétique du facteur de qualité.
On considère un circuit RLC série de facteur de qualité
o
L
QR
avec
1
oLC
.
1. Exprimer l'énergie emmagasinée à l'instant t, notée E (t) dans un dipôle RLC en régime sinusoïdal forcé, en fonction de
l'amplitude Im de l'intensité, du temps t et des caractéristiques du montage (L, C et ). Vous travaillerez avec les grandeurs
sinusoïdales et on prendra i(t) = Im cos (t) pour l’intensité du courant traversant le circuit.
2. Vérifier que E (t) est indépendante du temps si l'on est à la résonance d'intensité du circuit.
Retrouver ce résultat par un bilan énergétique.
3. Dans le cas général (différent du 2), calculer la moyenne temporelle <E (t)> ainsi que l'énergie WJ reçue (et dissipée) par la
résistance en une période.
4. Exprimer le rapport <E (t)>/W en faisant apparaître le facteur de qualité et la pulsation réduite /o.
Proposer une interprétation énergétique du facteur de qualité.
C
u(t)
R
L
r
C
u(t)
L’
R
L
A
B
C
i
e
D
DG