Fonctions puissances

Analyse | 1
 Fonctions usuelles 
Logarithme népérien et exponentielle
Définition
* La fonction logarithme népérien, notée ln est l’unique primitive sur 
 de    qui s’annule en 1. Elle est donc défini
sur 
 par   
* La fonction exponentielle est la fonction réciproque de la fonction logarithme népérien
ln o exp = exp o ln = Id
Ensemble de définition
La fonction ln est défini sur 
 et la fonction exp est défini sur 
Continuité et dérivabilité
Les fonctions ln et exp sont continues et dérivables sur leur ensemble de définition
 et     
Variations et limites
Les fonctions ln et exp sont des bijections strictement croissantes
    et 
   et 
Transformation somme / produit
 (si on sait que xy > 0 mais on ne connaît pas le signe de x et y)
Graphe

Analyse | 2
Fonctions puissances
Définition
On appelle fonction puissance toute fonction du type x  x 
Propriétés
Soient x, x’  
 et y, y’  
 et  
Ensemble de définition
L’ensemble de définition de x  x  est 
Continuité et dérivabilité
La fonction x  x est continue et dérivable sur son ensemble de définition.
Sa dérivée est la fonction x  x-1
Variations et limites
Si α > 0 la fonction x  xα est strictement croissante et 
  et 
Si x  x est strictement décroissante et 
  et 
Si α = 0, la fonction x  x est constante égale à 1
Bijectivité
Pour α 0, la fonction réalise une bijection de 
 sur  . Sa bijection réciproque est la fonction  
Graphes

Analyse | 3
Fonctions circulaires directes
Définition
On appelle fonctions circulaires ou trigonométriques directes les fonctions
sin, cos et tan
* tan se retrouve grâce à Thalès
Ensemble de définition
Les fonctions sin et cos sont définies sur . La fonction tan est définie sur \
Parité
La fonction cos est paire. Les fonctions sin et tan sont impaires
Périodicité
Les fonctions sin et cos sont 2-périodiques. La fonction tan est -périodique.
Continuité et dérivabilité
Les fonctions sin, cos et tan sont continues et dérivables sur leur intervalle de définition.
sin' = cos cos’ = -sin tan’ = 1 + tan² = 1/cos²
Graphes
Equations trigonométriques
On appelle équations trigonométriques des équations faisant intervenir les fonctions trigonométriques. L’idée est de se
ramener à une des trois équations types suivantes dont la solution se retient aisément grâce à un dessin.

Analyse | 4

Analyse | 5
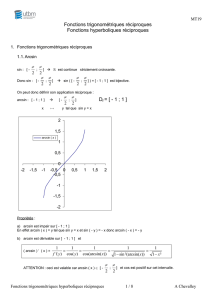
Fonctions circulaires réciproques
Définitions
La fonction sin induit une bijection strictement croissante de 
 sur [-1, 1].
On appelle la fonction arcsinus sa fonction réciproque notée arcsin
La fonction cos induit une bijection strictement décroissante de  sur [-1, 1].
On appelle la fonction arccosinus sa fonction réciproque notée arccos
La fonction tan induit une bijection strictement croissante de 
 sur .
On appelle la fonction arctan sa fonction réciproque notée arctan
Ensemble de définition et image
Les fonctions arcsin et arccos sont définies sur [-1, 1] et la fonction arctan est définie sur .
L’image de arcsin est 
L’image de arccos est 
L’image de arctan est 
Variations et limites
Les fonctions arcsin et arctan sont strictement croissantes. La fonction arccos est strictement décroissante.
Parité
Les fonctions arcsin et arctan sont impaires.
La fonction arccos n’est ni paire ni impaire. On a néanmoins la relation pour x  [-1, 1] arccos(-x) =  – arccos x
Continuité et dérivabilité
Les fonctions arcsin, arccos, et arctan sont continues sur leur ensemble de définition.
Les fonctions arcsin, arccos sont dérivables sur ]-1, 1[ et la fonction arctan est dérivable sur 
Graphes
Les courbes de arcsin et arccos admettent des tangentes verticales en -1 et 1
(arcsin et arccos ne sont pas dérivables en -1 et 1)