Quadripoles Electrique

Université Moulay Ismail
Faculté des Sciences et Techniques Err achidia
Département de Physique
Année universitaire 2008 – 2009
Deuxième semestre
1
Pr. Omar El outassi
www.geocities.com/eloutassiomar
Quadripôle électrique
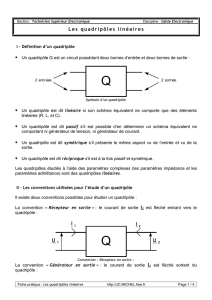
1- Définition et représentation :
Un quadripôle électrique est un circuit électrique qui admet deux bornes
d’entrées et deux bornes de sorties (figure 1). En effet, nous utilisons
la représentation de quadripôle pour tout circuit électrique ou
électronique complexe. Les grandeurs électriques du quadripôle sont :
Les courants, d’entrée et de sortie
21,II
et les tensions, d’entrée et de
sortie
21,UU
Les courants qui pénètrent dans le quadripôle sont par convention dans
le sens positif.
Figure 1
Remarque :
Si dans un quadripôle une borne d’entrée est liée à une borne de sortie
ce dernier est dit tripôle électrique. (Un transistor par exemple)
2- Matrices représentatives des quadripôles
Dans le cas d’un quadripôle linéaire les grandeurs d’entrée et de sortie
peuvent êtres exprimées sous plusieurs formes selon les cas :
a- Matrice Impédance :
Tels que :
2
1
2221
1211
2
1I
I
ZZ
ZZ
U
U
2221
1211 ZZ
ZZ
est la matrice impédance du quadripôle.
22211211 ,,, ZZZZ
sont des impédances du quadripôle.
b- Matrice admittance :
Tels que :
2
1
2221
1211
2
1U
U
AA
AA
I
I
2221
1211 AA
AA
est la matrice admittance du quadripôle.
22211211 ,,, AAAA
sont des admittances du quadripôle.
b- Matrice de transfert :
Tels que :

Université Moulay Ismail
Faculté des Sciences et Techniques Err achidia
Département de Physique
Année universitaire 2008 – 2009
Deuxième semestre
2
Pr. Omar El outassi
www.geocities.com/eloutassiomar
1
1
2221
1211
2
2I
U
TT
TT
I
U
2221
1211 TT
TT
est la matrice de transfert du quadripôle.
22211211 ,,, TTTT
sont des paramètres du quadripôle tels que :
11
T
et
22
T
sont des
nombres,
12
T
est une impédance,
21
T
est une admittance.
c- Matrice hybride :
Tels que :
2
1
2221
1211
2
1U
I
HH
HH
I
U
2221
1211 HH
HH
est la matrice Hybride du quadripôle dont l’intérêt est
primordiale pour l’étude des transistors.
22211211 ,,, HHHH
sont des paramètres du quadripôle tels que :
21
H
et
12
H
sont des nombres,
11
T
est une impédance,
22
T
est une admittance.
3- Associations de quadripôle :
a- association en cascade :
Soit n quadripôles associées en cascade tel que les grandeurs de sortie
du (i-1)ème sont les grandeurs d’entrée du ième. Voir figure 2
Figure 2
Dans ce cas d’associations il est plus commode d’utiliser les matrices
de transfert des quadripôles pour alléger le calcul.
i
i
i
i
i
i
i
ii
i
i
I
U
T
I
U
TT
TT
I
U
1
1
1
1
2221
1211
2
2
i
T
est la matrice de transfert du ième
quadripôle.
1
1
1
1
1
1
1
2
2
i
i
i
i
i
I
U
T
I
U
1i
T
est la matrice de transfert du (i-1)ème quadripôle.
Avec
i
i
i
i
I
U
I
U
1
1
1
2
1
2
, alors
1
1
1
1
1
1
2
1
2
1
1
2
2
i
i
ii
i
i
i
i
i
i
i
i
I
U
TT
I
U
T
I
U
T
I
U
, faisons le
même calcul pour tous les quadripôles en cascade, on obtient :
1
1
1
1
1
11
1
1
1
2
1
2
1
1
2
2I
U
T
I
U
TT
I
U
T
I
U
T
I
U
ni i
n
n
nn
n
n
n
i
n
n
n
n

Université Moulay Ismail
Faculté des Sciences et Techniques Err achidia
Département de Physique
Année universitaire 2008 – 2009
Deuxième semestre
3
Pr. Omar El outassi
www.geocities.com/eloutassiomar
Remarque :
La
1
ni i
T
n’est pas commutative.
Exemple : Quadripôle en T
Soit le circuit de la figure 3.
En utilisant le raisonnement précédant on
peut écrire :
1
1
123
1
1
2
2I
U
TTT
I
U
T
I
U
i
n
n
Avec :
10
11
1Z
T
,
1
101
2
2Z
T
,
10
13
3Z
T
Figure 3
Nous obtenons alors :
2
1
2
3
2
13
1
2
3
11
1
1
Z
Z
Z
Z
ZZZ
Z
Z
Z
T
b- association en série :
Soit l’association des quadripôles de
la figure 4 : Les courants ‘entrée et
de sorties restent les mêmes.
Cependant, les tensions s’ajoutent.
Dans ce cas d’association nous
utilisons la matrice impédance pour
alléger le calcul.
n
i
n
UUe11
et
n
i
n
sUU 12
Or
2
1
2
1
I
I
Z
U
U
i
i
i
donc :
  2
1
11 2
1
I
I
Z
U
U
U
Un
ii
n
ii
i
s
e
,
alors :
n
iieq ZZ 1
Figure 4

Université Moulay Ismail
Faculté des Sciences et Techniques Err achidia
Département de Physique
Année universitaire 2008 – 2009
Deuxième semestre
4
Pr. Omar El outassi
www.geocities.com/eloutassiomar
C- association en parallèle :
Dans le cas de l’association en parallèle, voir figure 5.
Dans ce cas les tensions d’entrée et
de sortie restent les mêmes et les
courants s’additionnent, il est alors
plus commode d’utiliser la matrice
admittance pour alléger le calcul.
n
i
n
IIe11
et
n
i
n
sII 12
Or
2
1
2
1
U
U
Z
I
I
i
i
i
donc :
  2
1
11 2
1
U
U
Y
I
I
I
In
ii
n
ii
i
s
e
,
alors :
n
iieq YY 1
Figure 5