Chapitre 27

MPSI Chapitre 27
LE CHAMP ÉLECTROSTATIQUE, LE POTENTIEL ÉLECTROSTATIQUE
27-1 Complément mathématique
27-1-1 Coordonnées sphériques
H étant la projection de M sur le plan xOy, les coordonnées sphériques du point M sont :
OMr
: coordonnée radiale,
  OM,Oz
: colatitude,
  OH,Ox
: longitude.
x = r sin cos , y = r sin sin et z = r cos.
sinucosuu yx
et
cosusinuu yx
.
cosusinuu zr
donc
  cosusinsinucossinuu zyxr
.
sinucosuu z
donc
sinusincosucoscosuu zyx
.
Un déplacement élémentaire s'écrit :
  udsinrudrudrMd r
.
Un petit volume élémentaire s'écrit :
 dddrsinrd 2
.
27-1-2 Gradient d'un champ scalaire
En coordonnées cartésiennes,
zyx u
z
F
u
y
F
u
x
F
Fgrad
.
y
dr
rd
dsinr
u
r
u
u
x
O
z
r
d
d
sinr
M
H
r
u
u
u
u
x
u
y
u
z
u
u
y
dr
rd
dsinr
u
r
u
u
x
O
z
r
d
d
sinr
M
H
r
u
u
u
u
x
u
y
u
z
u
u

Pour un champ scalaire stationnaire F = f(x,y,z) :
Md)F(graddF .
(définition intrinsèque).
La définition intrinsèque du gradient permet d'obtenir son expression dans le différents systèmes de
coordonnées :
En coordonnées cylindropolaires (r,,z),
dz
z
F
d
F
dr
r
F
dF 
et
  zr udzudrudrMd
donc
zr u
z
F
u
F
r
1
u
r
F
Fgrad
.
En coordonnées sphériques (r,,),
d
F
d
F
dr
r
F
dF
et
  udsinrudrudrMd r
donc
u
F
sinr 1
u
F
r
1
u
r
F
Fgrad r
.
27-1-3 Propriétés de l'opérateur gradient
Il s'agit d'un opérateur linéaire car, si a, b, c sont indépendant de la position de M :
...HgradcGgradbFgrada);;;cHbGaF(grad  
La définition intrinsèque du gradient donne dF =
 Md,FgradcosMdFgrad
, donc dF est
maximal si le déplacement de M est orienté comme le gradient de F.
Le gradient d'un champ scalaire est donc orienté dans la direction et dans le sens dans lesquels la
croissance du champ est maximale.
Les surfaces de niveau d'un champ scalaire sont les surfaces sur lesquelles F est uniforme. Soit un
déplacement élémentaire
Md
sur une surface de niveau, on a :
0Md)F(graddF . 
donc
 MdFgrad
.
Le gradient d'un champ scalaire F est normal aux surfaces de niveau et orienté dans le sens F
croissant.
27-1-4 Champ de gradient, potentiel scalaire
G
est un champ de gradient
)F(gradG:F  
. F est le potentiel scalaire dont dérive
G
.
F n'est ainsi défini qu'à une constante additive près car
)F(grad)KF(grad  
, si K est une constante.
La circulation d'un champ de gradient sur une courbe , de M1 à M2 est indépendante du chemin 
suivi de M1 à M2 :
21
M
M
M
MFFdFMdG 2
1
2
1.
.
Un champ de gradient a une circulation conservative.
La circulation d'un champ de gradient est la diminution du potentiel dont il dérive.
Par exemple, une force conservative (indépendante du temps) dérive d'un potentiel appelé énergie
potentielle car son travail est la diminution de cette énergie potentielle :
21
M
M
M
MEpEpdEpMdFW)Ep(gradF 2
1
2
1.
.
fgrad
F1F2 > F1
fgrad
F1F2 > F1

27-1-5 Vecteurs surfaces élémentaires, flux d’un champ vectoriel
Pour chaque portion élémentaire d’aire dS de la surface , s’appuyant sur un contour orienté 
(contour fermé) , on définit un vecteur surface élémentaire
Sd
tel que :
-
Sd
,
-
dSSd 
,
-
Sd
est orienté dans le sens lié au sens de rotation sur le contour  par les règles pratiques
habituelles : règle du tire-bouchon, face sud vers face nord...
Si la surface est fermée, les vecteurs
Sd
sont tous orientés vers l’extérieur du volume que cette
surface délimite.
Pour un champ vectoriel
G
, le flux à travers la surface  est ;
 SdG.
Si la surface  est fermée le flux est noté
 SdG.
.
Si le flux de
G
est nul à travers toute surface fermée, alors il est le même à travers toute surface
s’appuyant sur un contour orienté donné et on dit que
G
a un flux conservatif.
27-2 Le champ électrostatique créé par une charge ponctuelle
27-2-1 Champ électrostatique
Soit une charge ponctuelle q placée au point O fixe.
Si en M se trouve une charge qM, elle subit de la part de q la force de Coulomb :
3
0
MOM4OMqq
F
. En
utilisant des coordonnées sphériques de centre O :
 r
urOM
et
2
0
rM r4 uqq
F
.
Le champ électrostatique créé par la charge q placée en M est donc (que qM soit ou non présente) :
2
0
r
Mr4 uq
qF
E
.
Sd
face nord face sud
Sd
face nord face sud

La circulation élémentaire de ce champ est
 MdE.
avec
  udsinrudrudrMd r
donc
r4 q
d
r
dr
4q
MdE
0
2
0
.
. C'est une différentielle totale exacte, donc :
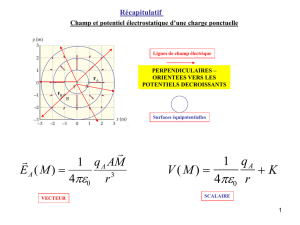
Le champ électrostatique créé par une charge ponctuelle fixe q placée en O à la distance r de O est
2
0
r
r4 uq
E
. Il n’est donc pas défini au point où se trouve la charge.
C'est un champ à circulation conservative, donc un champ de gradient.
Il dérive du potentiel électrostatique
r4 q
V
0
, (choisi avec
0Vlim
r
). V n’est donc pas défini
au point où se trouve la charge.
On a donc :
)V(gradE  
.
27-2-2 Surfaces équipotentielles, lignes de champ
Les surfaces de niveau de V sont les surfaces équipotentielles définies par r constante, ce sont les
sphères de centre O.
Les lignes de champ sont les lignes auxquelles
E
est tangent en chaque point .
Pour une charge ponctuelle ce sont les demi droites issues de O. Elles sont orientées dans le sens
centrifuge si q > 0 et centripète si q < 0.
Les tubes de champ sont donc les cônes de sommet O.
27-2-3 Flux du champ créé par une charge ponctuelle à travers une surface fermée
Si la surface  est fermée le flux du champ électrostatique est :
 SdE.
.
Pour le champ créé par une charge ponctuelle placée au centre O d’une sphère  de rayon R, le flux
de
E
à travers  est :
 SdE.
avec
2
0
r
R4
uq
E
et
 r
udSSd
donc
2
2
0
2
0
R4
R4 q
dS
R4 q
soit
0
q
.
On peut démontrer en utilisant la notion d’angle solide que ce résultat est général :
À travers toute surface fermée , le flux créé par une charge ponctuelle q est :
0
q
si la charge est à l’intérieur du volume délimité par .
 = 0 si la charge est extérieure à ce volume.
O
(q<0)
O
(q<0)

27-3 Champ et potentiel électrostatiques créés par une distribution de charges
27-3-1 Principe de superposition
Les forces électrostatiques subies par une charge qM placée en M de la part des charges qi placées
aux points Pi s’additionnent; l’effet électrique de qi sur qM n’est pas perturbé par la présence des autres
charges.
Ce principe est vérifié par toutes ses conséquences.
27-3-2 Champ et potentiel électrostatiques créés par une distribution de charges ponctuelles
Avec les notations ci-dessus, le champ que créerait en M la charge qi si elle était seule serait
3
10
ii
M
M/P
iMP4 MPq
q
F
Ei
et il dériverait du potentiel
MP4 q
V
i0
i
i
.
Le champ électrostatique en M, créé par la distribution de charges {Pi,qi} est
ii
M
iM/P E
q
F
Ei
.
Le principe de superposition s’applique donc au champ électrostatique.
La linéarité de l’opérateur gradient et
i
iVgradE  
impliquent que le principe de superposition
s’applique aussi au potentiel électrostatique : On a
VgradE  
, avec
ii
VV
.
On a donc (même en l’absence de charge électrique en M) :
i3
i
ii
0MP MPq
41
E
et
ii
i
0MP
q
41
V
. (Avec
MP
MP
ui
i
i
,
i2
i
i
i
0MP
uq
41
E
).
27-3-3 Champs et potentiels créés par des distributions de charges volumiques, surfaciques, ou
linéiques.
En admettant que l’on puisse décomposer un volume chargé V , avec la densité volumique de charge 
en P, ( est fonction des coordonnées de P, mais pas du temps), en charges quasi ponctuelles dq =  d, le
champ et le potentiel créés au point M sont :
V3
0PM
PMd
41
E
et
VPM
d
41
V
0
.
De même, pour la surface chargée , avec la densité surfacique de charge  en P :
3
0PM
PMdS
41
E
et
PM
dS
41
V
0
.
Pour une ligne  chargée avec la densité linéique de charge  en P :
3
0PM
PMdL
41
E
et
PM
dL
41
V
0
.
Si des distributions de charges de types différents (par exemple, charges ponctuelles et surfaciques) se
superposent, il faut additionner les contributions de ces distributions.