FACULTE DES SCIENCES DE TUNIS 2009

FACULTE DES SCIENCES DE TUNIS 2009-2010
DEPARTEMENT DE PHYSIQUE Série n°4
LFPH2
TRAVAUX DIRIGES DE MECANIQUE DES FLUIDES
Exercice 1
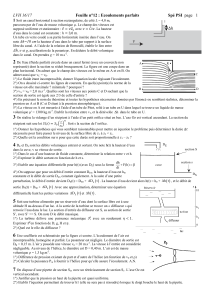
Pour vider l’eau d’un réservoir de section SR, on
utilise un siphon formé d’un tube coudé de section
intérieure S (S<<SR), terminé par un embout de section s
(voir figure). On supposera que l’eau se comporte comme
un fluide parfait, incompressible et que l’écoulement est
permanent.
On prendra Po=1bar, pour la pression atmosphérique.
1°/ Calculer la vitesse d’écoulement en F à l’extrémité de
l’embout.
2°/ Calculer le débit volumique du siphon.
3°/ Calculer la vitesse d’écoulement en B. Déduire la pression en B et la comparer à la pression en A.
4°/ Déterminer la pression en C et déduire la condition pour que le siphon puisse fonctionner.
On donne : S=7cm2 ; s=5cm2 ; zA=zB=zD=3,2m ; zC=4,2m ; zE=zF=0.
g=9,8 m/s2 ; masse volumique de l’eau : ρ=103kg/m3.
Exercice 2
Un réservoir cylindrique de rayon R, d’axe vertical, posé sur un plan horizontal, est
rempli jusqu’à une hauteur H d’eau, supposée fluide parfait incompressible de masse volumique
ρ. On perce la surface latérale du réservoir d’un trou circulaire, de rayon r telle que r <<R et
dont le centre se trouve situé à la distance h du niveau supérieur de l’eau. Grâce à une
alimentation permanente, on maintient constant le niveau de l’eau dans le réservoir.
1°/ Calculer la vitesse horizontale V0 de l’eau à la sortie de l’orifice.
2°/ Etablir dans le plan xoy les lois horaires (x(t) et y(t)) du mouvement d’une particule fluide
entre la sortie de la particule fluide de l’orifice et son impact au point P avec le plan horizontal.
3°/ Etablir l’équation de la trajectoire de la particule fluide entre sa sortie et son impact sur le
plan horizontal au point P.
4°/ En déduire l’expression de la distance L=OP. (O étant l’origine du repère)
5°/ Etudier les variations de la distance L en fonction de la distance h et tracer la courbe de
variation L(h).
Pour quelle valeur hm de h, la longueur L prend sa valeur maximale ?

Exercice 3
Une conduite cylindrique de section circulaire de diamètre D et d’axe horizontal de
vecteur unitaire , est raccordée à un tube fin de même axe, et de diamètre d<D et dont l’autre
extrémité est ouverte vers l’extérieur ( voir figure-a ). La conduite est fermée par un piston (C)
de masse négligeable, qui se déplace sans frottement. La conduite et le tube sont remplis d’un
liquide, supposé parfait, de masse volumique ρ constante.
Sous l’action d’une force = f , exercée par un opérateur extérieur, le piston ( C ) se
déplace très lentement, de façon uniforme, dans le même sens que avec une vitesse constante
= V pendant que le liquide sort du tube avec une vitesse = v (on suppose que les lignes
de courant à la sortie du tube sont parallèles à l’axe de la conduite).
On désigne par P la pression dans la conduite, et par P0 la pression dans le tube fin, supposée
égale à la pression extérieure, et on pose ΔP =P- P0.
1.
1°/ Par application de la loi de conservation du débit, établir une relation entre V, v, D et d.
2°/ En appliquant le théorème de Bernoulli, exprimer ΔP en fonction de ρ, v, D et d.
3°/ En déduire la force que l’opérateur exerce sur le piston.
4°/ En supposant que d<<D, donner la vitesse de l’écoulement v à la sortie du tube en fonction
de ρ et ΔP.
5°/ On place la conduite en position verticale (voir figure-b) et on enlève le piston (C), calculer
la vitesse de sortie du liquide et indiquer pour quelle hauteur h du liquide par rapport à
l’extrémité inférieure du tube, la nouvelle vitesse de sortie v sera la même que celle calculée à la
quatrième question.
Exercice 4
Une conduite cylindrique horizontale, de diamètre D = 25 cm, est parcourue par un
écoulement d’eau à vitesse uniforme VA ; elle présente un rétrécissement qui la raccorde à une
deuxième conduite cylindrique de diamètre d = 7,5 cm. Les extrémités d’un tube en U contenant
du mercure sont reliées aux deux conduites précédentes (voir figure)
X0 = 20cm
Hg
P0
Figure-b
P0
P0
h
(C)
P
P0
Figure-a
D A
B d

1°/ Sachant que la dénivellation entre les surfaces de séparation eau-mercure est X0 = 20 cm,
calculer la différence de pression ente les points A et B.
2°/ Calculer la vitesse de sortie VB et en déduire le débit volumique d’eau dans la conduite.
On donne :
3,0
D
d
;
33
eau m.kg10 
;
33
Hg 13,6 10 kg.m
;
2
s.m8,9g 
.
Exercice 5
Un jet de fluide, considéré incompressible et parfait, est envoyé sur une plaque plane
avec une vitesse
v
, un débit massique Dm et un angle d’incidence α.
L’écoulement est permanent dans le référentiel d’étude rattaché à la base orthonormé (
zyx e ,e ,e
),
z
e
étant normal à la plaque et
x
e
dans le plan d’incidence, défini par
z
e
et la vitesse du jet
incident.
Lors de l’impact sur la plaque, le jet incident se sépare en deux jets unidimensionnels,
dont les vitesses sont tangentes à la plaque et situées dans le plan d’incidence.
On suppose que l’influence de la pesanteur est négligeable et que le jet et la plaque sont
soumis à la pression atmosphérique.
Déterminer :
1°/ Les vitesses
1
v
et
2
v
des jets émergeants.
2°/ leurs débits massiques Dm1 et Dm2.
3°/ La force de poussée
F
exercée par le jet sur la plaque. Nous pouvons définir cette force
comme opposée à la force supplémentaire
0
F
qui est appliquée pour maintenir la plaque
immobile.