Physique : p 179 n° 6-7-8-10-12

1ère S – correction du DM des vacances de février 2004 18/04/2017
1/2
Physique : p 179 n° 6-7-8-10-12
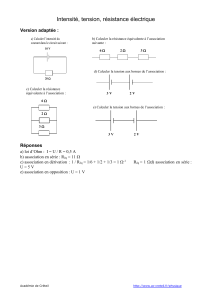
Exercice n° 6 :
a) La puissance électrique fournie par le générateur aux dipôles montés en
dérivation à ses bornes est : Pel = P1 + P2 = 50 + 150 = 200 W
b) Pel = UPN  I = (E – r  I)  I = E  I car r = 0 
(la résistance interne du générateur est négligeable)
Donc I =
E
Pel
=
12
200
= 16,7 A
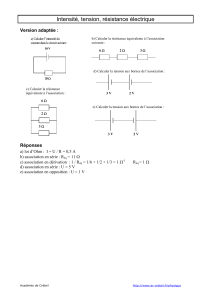
Exercice n° 7 :
a) La puissance électrique reçue par chaque dipôle AB est : Pel = UAB  I .
Comme les dipôles sont des conducteurs ohmiques, UAB = R  I.
Ainsi Pel = UAB  I = R  I². D’où I =
R
P
el
=
15
4,2
= 0,4 A = 400 mA.
Et UAB = R  I = 15  0,4 = 6 V
b)
La tension U aux bornes du générateur
vaut : U = U1 + U2 = 12 V
La force électromotrice E du générateur
vérifie E = U + r  I = U car r = 0 .
Donc E = 12 V
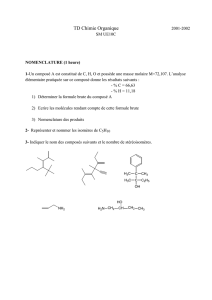
Exercice n° 8 :
a) La puissance électrique reçue par la lampe est : Pel = UAB  I (c’est aussi la puissance
électrique cédée par le générateur). Donc I =
AB
U
Pel
=
12
24
= 2,0 A
b) La puissance dissipée dans le générateur par effet Joule vaut : PJoule = r  I² (car I est aussi
l’intensité du courant qui circule dans la branche du générateur) : PJoule = 2,0  2,0² = 8,0 W.
La puissance totale P fournie par le générateur est la somme de la puissance électrique et de la
puissance Joule : P = Pel + Pjoule = 24 + 8 = 32 W
c) P = E  I d’où E = P/I = 32/2 = 16 V
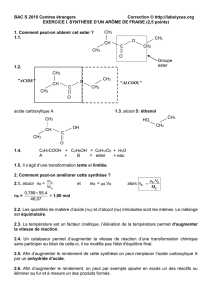
Exercice n° 10 :
a) La puissance électrique fournie par le générateur est Pgéné = UPN  I = (E – r  I)  I
La puissance électrique reçue par le conducteur ohmique et dissipée par effet Joule
est : Pjoule = R  I²
Comme le circuit ne comporte que le générateur et le conducteur ohmique et comme
les fils de connexion sont parfaits, toute la puissance du générateur est reçue par le
conducteur. Donc Pgéné = Pjoule.
Ainsi : (E – r  I)  I = R  I² soit encore (si I  0) : E – r  I = R  I
d’où E = (R + r)  I. Ce qui permet d’exprimer I : I =
Rr E
b) Pgéné = Pel = UPN  I = (E – r  I)  I = E  I – r  I² =
Rr
²E
-
)²Rr(
²Er
. En réduisant au même dénominateur, en
développant et en simplifiant : Pel =
)²Rr(
²E)Rr(
-
)²Rr(
²Er
=
)²Rr(
²ER
Application numérique : Pel =
)²102(
²610
= 2,5 W
c) L’association en dérivation de deux conducteurs ohmiques identiques équivaut à un conducteur ohmique équivalent de
résistance Réq vérifiant :
R
2
R
1
R
1
R1
éq 
donc Réq = ½ R.
Il suffit de reprendre l’expression précédente en replaçant la valeur de R par Réq.
Application numérique : Pel =
)²52(
²65
= 3,7 W. La puissance électrique n’est pas doublée car le fait de placer la 2ème
résistance en dérivation n’a pas fait doubler la résistance totale du circuit. Par ailleurs, bien que la résistance soit divisée
par deux, la puissance électrique fournie n’est pas non plus réduite à la moitié car Pel n’est pas proportionnelle à R.
+ G -
M
P1 = 50 W
P2 = 150 W
E = 12 V
P
N
I
+ G -
Pel = 2,4 W
R = 15 
E ; r = 0
R = 15 
Pel = 2,4 W
I
A
B
+ G -
E ; r = 0
I
U1 = 6 V
U2 = 6 V
+ G -
Pel = 24 W
r = 2,0 
P
N
I
U = 12 V
A
B
+ G -
R = 10 
E = 6,0 V ; r = 2,0 
I
P
N

1ère S – correction du DM des vacances de février 2004 18/04/2017
2/2
Exercice n° 12 :
Toutes les résistances sont identiques. Pour trouver la résistance équivalente aux différentes associations, il faut réduire
progressivement les associations en traitant d’une part les résistances en série et d’autre part celles en dérivation. Pour repérer
si des résistances sont en série ou en dérivation, il faut d’abord repérer les nœuds du circuit ( ) . Les résistances qui ne sont pas
séparées par un nœud sont en série, celles qui sont entre les deux mêmes nœuds sont en dérivation.
a)
équivaut à équivaut à Réq vérifie
R3
1
R
1
R1
éq 
=
R3
4
d’où Réq = ¾ R
b)
équivaut à équivaut à
équivaut à avec R1 = 2R + ¾R =
4
11
R équivaut à avec
R11
4
R
1
R1
éq 
=
R11
15
d’où Réq =
15
11
R
c)
équivaut à équivaut à avec
R2
1
R
1
R
1
R1
éq 
=
R2
5
d’où Réq =
5
2
R
Chimie : p 141 n° 6-7-8-10-11-22
Exercice n° 6 :
a) éthane b) propane c) méthylpropane d) méthylbutane e) 2,2-diméthylbutane
Exercice n° 7 :
a) voir c) exercice précédent b) voir e) exercice précédent
c) CH3  CH  CH2  CH  CH3 d) CH3  CH2  CH  CH2  CH3
CH3 CH3 CH2  CH3
Exercice n° 8 :
a) 2,3-diméthylpentane b) 3-méthylpentane c) 2,3-diméthylpentane
Exercice n° 9 :
a) pentane b) 2-méthylpentane c) 2,4-diméthylpentane d) 2,2-diméthylpentane
Exercice n° 10 :
a) b) c) d)
Exercice n° 11 :
C5H12 isomères du pentane
CH3  CH2  CH2  CH2  CH3
pentane
CH3  CH  CH2  CH3
CH3 méthylbutane
CH3
CH3  CH  CH3
CH3 diméthylpropane
Exercice n° 22 :
a) Si les gaz sont considérés comme parfaits, les pourcentages en volume sont identiques aux pourcentages en quantités car dans
les mêmes conditions de température et de pression, les quantités n sont proportionnelles aux volumes n =
TRP
V.
Donc une mole de gaz de Gröninge contient 0,81 mol de méthane, 0,03 mol d’éthane, 0,005 mol de propane, 0,145 mol de diazote
et 0,01 mol de dioxyde de carbone.
M = 0,81Mméthane + 0,03Méthane + 0,005Mpropane + 0,145Mdiazote + 0,01Mdioxyde de carbone
M = 0,8116 + 0,0330 + 0,00544 + 0,14528 + 0,0144 = 18,58 g.mo-1
b) d = masse molaire de ce mélange/ masse molaire de l’air dans les mêmes conditions = 18,58/29 = 0,64
La densité n’a pas d’unité
R
R
R
R
3R
R
Réq
R
R
R
R
R
R
R
R
R
R
3R
R
R
R
R
¾R
R1
R
R
4
11
R
Réq
R
R
R
R
R
2R
R
Réq