Graphiques de l`étude de la chute avec frottement d`une bille

Terminale S TP de Physique
Objectifs
Utiliser une méthode numérique itérative (méthode d’Euler) pour résoudre l’équation différentielle caractéristique de
l’évolution d’un système mécanique à l’aide d’un tableur.
I. Première approche.
L’étude de l’évolution temporelle d’un système matériel mécanique conduit à mesurer le taux de variation de certaines grandeurs
physiques.
Le taux de variation d'un déplacement est une vitesse.
Le taux de variation d'une vitesse est une accélération.
Ce taux de variation instantané est représenté par une dérivée.
L'objet mathématique qui décrit l'évolution temporelle du système est une équation différentielle.
Résoudre une équation différentielle, c’est rechercher une fonction, afin de prévoir l’évolution de ce système. Cela passe par la
connaissance :
- des conditions initiales qui définissent l'état du système à une date antérieure,
- des lois d’évolution qui mettent en jeu les actions (forces) qui s’exercent sur le système.
II. La situation-problème.
A la date t = 0, un solide de masse m et de volume V est abandonné dans l'air l'altitude z.
Quelles sont les caractères du mouvement de chute verticale de ce solide dans le champ de pesanteur uniforme ?
1. Quelle est l'équation différentielle du mouvement ?
 Les actions sur ce solide sont :
- le poids (on admettra que g = g0 = 9,8 N.kg-1 dans le domaine considéré).
- la poussée d'Archimède (que l'on négligera ici).
- la force de frottement fluide dont la valeur est proportionnelle à la vitesse.
(k>0 est le coefficient de frottement fluide pour le solide étudié).
 Dans le référentiel terrestre galiléen, la deuxième loi de Newton appliquée
au solide régit le mouvement de son centre d'inertie G.
 Dans le repère Oz , vertical, orienté vers le haut :
Fz + Pz = m.az soit : -k.vz - m.g = m.az
ou az + (k/m).vz + g = 0
Cette relation peut s'écrire :
soit : z"(t) + (k/m).z’(t) + g = 0 (équation différentielle du second ordre)
2. Quelle est la méthode de résolution numérique ?
22. Étude de la chute
verticale d’un solide avec
frottement
P = m.g
F = -k.v
F + P = m.aG
F
P
O
z
g
G
dz
dt
d2z
dt2
+ (k/m). + g = 0
PA = -'air.V. g

Considérons l'équation différentielle : az(t) + (k/m).vz(t) + g = 0
 A la date ti , admettons que l'on connaisse les valeurs de vz et de z (soient vi et zi ).
Calcul de az : ai = -(k/m).vi – g
 A la date ti+1 = ti + t , quelles sont les nouvelles valeurs de vz et de z ?
Admettons que pendant la durée t (pas de discrétisation temporelle ou pas de résolution), on puisse considérer az = cte = ai
Calcul de vz : vi+1 = ai.t + vi
Calcul de z : zi+1 = 0,5.ai.t2 + vi.t + zi
Ces nouvelles valeurs de vz et de z nous servent à initialiser un nouveau calcul de az ...etc...
En résumé :
Indication : Le premier calcul de az est effectué à partir des conditions initiales (t0 , v0 , z0) figurant dans l'énoncé du
problème.
3. Résolution à l'aide du tableur Excel.
On se propose de modéliser la chute verticale d'une goutte d'eau (supposée sphérique) dans l'air au cours des 20 premières secondes
de sa chute.
a) Préparation de la feuille de calcul.
 Ouvrir le fichier chutefrottement.xls présent dans le répertoire TS.
 Dans un premier tableau ont été entrées :
- les données numériques (m; k; g)
- les conditions initiales du mouvement (t0; v0; z0)
Y ajouter le pas de discrétisation temporelle (t) réglable à l'aide d'un bouton.
Il doit pouvoir être réglé entre 0,05s à 6,00 s avec une précision de 0,05s
Indications : Faire apparaître le menu « boite à outils contrôles » par un clic droit sur la zone grisée de la barre d’icones
d’Excel. Choisir le bouton de type « Barre de défilement » et tracer, par cliquer-glisser ce bouton sur la feuille de calcul à la
droite du tableau. Cliquer alors sur l’icône propriétés pour définir les caractéristiques de cette barre de défilement. Régler Min
sur 5, Max sur 600 et le défilement (SmallChange) sur 5. Entrer J8 en tant que cellule associée (LinkedCell). Désactiver le
mode création en cliquant sur la première icône de la boite d’outils contrôles. Actionner la barre pour vérifier son bon
fonctionnement. Entrer alors la formule dans la cellule « pas » du tableau pour qu’il varie de 0,05 à 6 s.
Remarque : Il est nécessaire d'utiliser une cellule intermédiaire (J8) car Excel ne permet pas de créer une barre de défilement
avec un pas (small change) inférieur à 1.
 Compléter le deuxième tableau avec :
colonne A : dates t calculées à partir de la valeur du pas de discrétisation temporelle.
- la première cellule reçoit la valeur de t0
- la deuxième reçoit la formule t1 = t0 + t
- Effectuer une recopie incrémentée de cette formule (i.e. recopier cette formule dans les 514 autres cellules de la colonne en
tirant la poignée dans le coin droit)
Conditions initiales
ti ; vi ; zi
calcul de
ai
calcul de
vi+1
calcul de
zi+1
itération
ti+1

Indication : L’adresse de la cellule où se trouve la valeur du pas t étant toujours G9, elle ne doit pas varier (on dit qu’elle
a une adresse absolue). Il faut donc l’écrire dans la formule donnant t sous la forme $G$9 et non G9.
colonne B : accélérations az déduites de l'équation différentielle du mouvement.
- la première cellule reçoit la formule a0 = -(k/m).v0 – g
- la deuxième reçoit la formule a1 = -(k/m).v1 – g
- recopier cette formule dans toutes les autres cellules (tirer la poignée dans le coin droit)
Indications : Distinguez bien adresses relatives et absolues de cellules dans ces formules.
colonne C : vitesses vz calculées en admettant que ai = Cte sur t
- la première cellule reçoit la valeur de v0
- la deuxième reçoit la formule v1 = a0. t + v0
- recopier cette formule dans toutes les autres cellules (tirer la poignée dans le coin droit)
colonne D : altitudes z calculées en admettant que ai = Cte sur t
- la première cellule reçoit la valeur de z0
- la deuxième reçoit la formule z1 = 0,5.a0. t2 + v0. t + z0
- recopier cette formule dans toutes les autres cellules (tirer la poignée dans le coin droit)
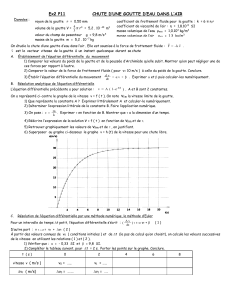
b) Insertion des graphiques associés.
En utilisant l'assistant graphique (mode nuage de points, affichage des courbes lissées sans points) dessiner successivement les
graphiques représentatifs des variations de az(t) , vz(t) , z(t).
Indication : Pour sélectionner deux colonnes non contiguës, utiliser la touche CTRL.
Placer ces 3 graphiques les uns sous les autres à droite du tableau. Pour que ce graphiques soient lisibles, il faut fixer une échelle
des temps qui soit la même pour tous. Pour ce faire, clic droit sur l’axe des temps du graphique az(t). Choisir « format de l’axe… »
et imposer 20 comme maximum. Faire le même travail pour les deux autres courbes. Pour la courbe z(t), imposer sur l’axe vertical
0 et 1000 comme minimum et maximum.
 Constater la présence de deux régimes de chute (régime initial, régime permanent asymptotique) et préciser comment varient
az(t) , vz(t) et z(t) durant ces 2 régimes.
 Augmenter la valeur du pas de résolution, observer les courbes. Discuter la pertinence des courbes obtenues et conclure.
 Le coefficient de frottement fluide est proportionnel au rayon de la goutte.
Si l'on double le rayon de la goutte, le coefficient k de frottement double aussi.
Comment la vitesse limite varie-t-elle alors ? (Effectuer la simulation en modifiant les données)
 Simuler une chute verticale dans le vide.
Vérifier, avec un pas suffisamment petit, que l'on retrouve la solution analytique de l'équation différentielle du mouvement.

FICHE T.P. 22 Résolution d’équations différentielles
Méthode d’Euler
Le programme prévoit uniquement la résolution numérique de l'équation différentielle correspondant à l'étude de la chute
verticale avec frottement.
Quelques données (d'après annales bac)
Poussée d'Archimède : PA = '.V.g
Coefficient de frottement fluide pour un solide sphérique : k = 6R
Force de frottement fluide : F = k.v
chute d'une goutte d'eau
dans l'air
chute d'une bille d'acier
dans la glycérine
Masse volumique du mobile
eau = 1,0.103 kg.m-3
acier = 7,8.103 kg.m-3
Masse volumique du fluide
'air = 1,3 kg.m-3
'glycérine = 1,3.103 kg.m-3
Viscosité de l'air
air = 1,8.10-5 kg.m-1.s-1
glycérine = 1,0 kg.m-1.s-1
Valeur du champ de pesanteur
g = 9,8 N.kg-1
g = 9,8 N.kg-1
Rayon de la goutte (ou bille)
R = 5,0.10-4 m
R = 1,5.10-3 m
Volume de la goutte (ou bille)
V = 5,2.10-10 m3
V = 1,4.10-8 m3
Masse de la goutte (ou bille)
m = 5,2.10-7 kg
m = 1,1.10-4 kg
Coefficient de frottement fluide
k = 1,7.10-7 kg.s-1
k = 2,8.10-2 kg.s-1
Poids de la goutte (ou bille)
P = 5,1.10-6 N
P = 1,1.10-3 N
Poussée d'Archimède
PA = 6,6.10-9 N
PA = 1,8.10-4 N
Les fichiers Excel proposés.
Chute verticale avec frottement
Chute d'une goutte d'eau dans l'air (feuille 1)
Chute d'une bille d'acier dans la glycérine (feuille 2)
Observation des courbes numériques a(t), v(t), z(t).
Chute libre verticale
Etude comparée de z(t) analogique et numérique
Décroissance radioactive
Evolution de la population moyenne d'un ensemble de noyaux radioactifs :
étude comparée de N(t) analogique et numérique.
Dipôle RC
Charge et décharge d'un condensateur à travers une résistance :
Etude comparée de uC(t) analogique et numérique.
Observation de i(t) numérique.
Dipôle RL
Etablissement et annulation du courant dans un circuit RL :
Etude comparée de i(t) analogique et numérique.
Oscillateur électrique RLC
Oscillations libres dans un circuit RLC série :
Observation des courbes numériques uC(t) et i(t)
Les trois régimes de fonctionnement.
Oscillateur mécanique
Oscillations libres d'un pendule élastique (solide – ressort) :
Etude comparée de x(t) analogique et numérique.

Annexe 1 : Préparation de la feuille de calcul Excel.
A
B
C
D
E
F
G
1
Chute verticale avec frottement fluide (F = k.v)
2
Méthode numérique (Euler)
3
4
Chute d'une goutte d'eau dans l'air (poussée d'Archimède négligeable)
5
Equation différentielle : z" + (k/m).z' + g = 0 (avec g = g0 = 9,8 m.s-2)
6
7
Données
Conditions initiales
pas
8
m (kg)
k (kg.s-1)
g (m.s-2)
t0 (s)
z0 (m)
v0 (m.s-1)
(en s)
9
5,2E-07
1,7E-07
9,8
0
1000
0
0,1
10
11
t
z" = az
z' = vz
z
12
(s)
(m.s-2)
(m.s-1)
(m)
13
0,0
-9,8
0,0
1000
A
B
C
D
E
F
G
10
11
t
z" = az
z' = vz
z
12
(s)
(m.s-2)
(m.s-1)
(m)
13
0,0
-9,8
0,0
1000
14
0.1
-9,5
-1,0
1000
=$D$9
=$F$9
=-(($B$9/$A$9)*C13)-$C$9
=$E$9
=A13+$G$9
=(0.5*B13*$G$9^2)+(C13*$G$9)+D13
=-(($B$9/$A$9)*C14)-$C$9
=-($B$8/$A$8)*C14-$C$8
=B13*$G$9+C13