Date - Notre physique - chimie au collège et au lycée

582693155 Page 1 sur 4 17/04/17
Date :
T2
Activités documentaires
ST3
RÉFÉRENTIELS ET VECTEURS
Activité 1
PROBLEMATIQUE
Il n’est pas possible d’affirmer qu’un objet est en mouvement ou au repos, ou qu’il est animé d’une vitesse grande ou
petite sans, dans un premier temps, s’intéresser au référentiel dans lequel on se place.
DOCUMENT : De la relativité de la vitesse
Donner une vitesse n’a aucun sens si on ne spécifie pas le
référentiel dans lequel on le mesure. Vous n’avez en
général pas besoin d’y penser dans la vie courante. Quand
le panneau de limitation indique 100 kilomètres/heure, on
comprend que notre vitesse est mesurée par rapport à la
route et non par rapport au trou noir situé au centre de la
voie lactée. Pourtant, même dans la vie courante, il arrive
que l’on doive se soucier du référentiel.
Par exemple, si vous avancez une tasse de thé à la main
dans le couloir d’un avion de ligne de vol, vous pouvez dire
que vous vous déplacez à 5 km/h. Quelqu’un au sol
pourrait dire que vous vous déplacez à 905 km/h. Avant de
décider lequel est le plus proche de la vérité, rappelez-
vous que, la Terre tournant autour du Soleil, un
observateur situé à la surface de ce dernier sera en
désaccord avec les deux affirmations et prétendra que
vous vous déplacez à environ 30 km/s, tout en enviant
votre climatisation.
The Grand Design, Stephen Hawking et Léonard Mlodinow, 2010.
Y a t-il un grand architecte dans l’univers?
Traduction Marcel Filoche, Odile Jacob, 1011
PISTES DE REFLEXION
1) A l’aide du document, et éventuellement de vos acquis des classes précédentes, proposer une définition du mot
référentiel.
2) Dans le second paragraphe du document :
a. Quel est l’objet dont on étudie le mouvement ?
b. Quelle est la grandeur, associée à cet objet, dont la valeur change ?
c. Quels sont les trois référentiels choisis par les auteurs ?
3)
a. Pour un observateur au sol, quelle est la vitesse de l’avion de ligne ?
b. En supposant que la Terre décrive un cercle (dont vous devez trouver la circonférence) de rayon 150 millions de
kilomètres en un an (365 jours) autour du Soleil, retrouver la valeur « 30 km/s »
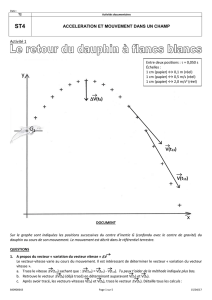
4) Étude de la figure
a. Quel est l’objet dont on étudie le mouvement dans la figure 1 ?
b. Quels sont les deux référentiels d’étude choisis ?
5) Lors du passage d’un référentiel à un autre, qu’est-ce qu’est modifié au niveau de l’objet d’étude ?
6) Pour conclure : pourquoi doit-on toujours préciser dans quel référentiel est étudié le mouvement d’un objet ?

582693155 Page 2 sur 4 17/04/17
Activité 2
DOCUMENT
Sur un graphe millimétré sont indiquées les positions successives du centre d’inertie G (confondu avec le centre de
gravité) du dauphin au cours de son mouvement. Une durée = 0,20 s s’écoule entre deux positions successives. Le
mouvement est décrit dans le référentiel terrestre auquel on associe le repère orthonormé habituel et un repère de
temps tel que à t = 0,00 s le point G est à l’origine.
QUESTIONS
1. A propos du vecteur-position
Le vecteur
OG
est appelé vecteur-position du point G. Les coordonnées de ce vecteur sont notées xG(t), yG(t) et zG(t) car
elles varient en fonction du temps t. Le mouvement a lieu dans le plan vertical d’où zG(t)= 0.
a. Relève sur le graphe les coordonnées du point G aux dates t6 = 1,20 s la date t8 = 1,60 s.
xG(t6) = yG(t6) = et xG(t8) = yG(t8) = .
b. Complète le graphe avec la position G15 du point G à la date t15 = à partir de leurs coordonnées
xG(t15) = 25,6 m et yG(t15) = 7,0 m.
2. A propos du vecteur-vitesse
Au cours de ce mouvement, le point G change de direction et de vitesse en permanence. Il est pratique de représenter
cette direction et cette vitesse par un vecteur-vitesse
G
v
. Le vecteur-vitesse
G
v
a la direction et le sens du
mouvement. Il est donc tangent à la trajectoire. La valeur vG de ce vecteur est toujours positive et s’exprime en m/s.
NB :
Les coordonnées du vecteur-vitesse dans le repère
k,j,i,O
sont notées vGx(t), vGy(t)et vGz(t). Elles peuvent être positives
ou négatives selon l’orientation du vecteur.
La longueur du vecteur-vitesse que l’on peut mesurer à la règle sur un schéma est proportionnelle à la valeur de la
vitesse grâce à une échelle. Attention, sur le graphe, une échelle est indiquée !
y
x
Échelles :
1 cm (papier) ↔ 2 m (réel)
1 cm (papier) ↔ 2,5 m/s (réel)
V(t2)
V(t13)

582693155 Page 3 sur 4 17/04/17
Comment déterminer la valeur du vecteur-vitesse connaissant la trajectoire ?
a. Mesure la longueur du vecteur vitesse du point G à la date t2 = 0,40 s. Déduis-en la valeur vG(t2) de la vitesse :
b. De la même manière, détermine la valeur vG(t13) de la vitesse de G à la date t13 = 2,60 s :
c. La vitesse instantanée vG(t13) à la date t13 est très proche de la vitesse moyenne entre les dates t12 et t14 car elles
sont très rapprochées. Par cette méthode, retrouve la valeur de la vitesse à cette date :
1214
1412
13Gtt
GG
)t(v 
=
Comment tracer le vecteur-vitesse sur la trajectoire ?
d. Regarde la méthode détaillée sur l’animation http://www.ostralo.net/3_animations/swf/vitesse.swf.
Résumé de la méthode :
Déterminer la valeur de la vitesse à la date ti avec :
Tracer le vecteur dans une direction tangente à la trajectoire et dans le sens du mouvement en tenant compte de
l’échelle de vitesse choisie.
e. Applique-la en traçant le vecteur-vitesse à la date t7 = 1,40 s.
Donne le détail du calcul :
f. Recommence avec le vecteur-vitesse à la date t10 = 2,00 s.
Donne le détail du calcul :
Quelles sont les coordonnées du vecteur-vitesse ?
g. Vérifie sur le graphe que vGx(t2) = 8,5 m/s et que vGy (t13) = -5,6 m/s.
h. Détermine les coordonnées vGx et vGy à la date t13 :
i. Pourquoi la coordonnée vGy(t14) est-elle négative ?
Retrouvons valeur du vecteur-vitesse à partir des coordonnées !
j. Retrouve la valeur de vG(t2) par le calcul à partir des coordonnées vGx(t2) = 10,0 m/s et vGy (t2) = -8,8 m/s.
1i1i
1i1i
iG tt
GG
)t(v

582693155 Page 4 sur 4 17/04/17
Activité 3
PROBLEMATIQUE
Lorsqu’un skieur utilise un téléski pour remonter une pente, sa vitesse peut varier, tout comme la force qui modélise
l’action de la perche du téléski sur lui. Existe-t-il un lien entre ces deux grandeurs ?
DOCUMENT
Le système étudié {skieur+ équipement} a une masse m = 85kg.
La piste est plane et, à l’altitude de la station de ski, l’intensité de pesanteur a pour valeur
g0 = 9,8 m.s-2. Sur la figure 2, la situation est modélisée.
Dans les figures 3 et 4, on représente les forces modélisant les actions mécaniques
s’exerçant sur le système dans deux situations différentes.
PISTES DE REFLEXION
1) Dans quel référentiel étudie-t-on le mouvement du système ?
2) Quelles actions mécaniques modélisent les forces représentées ?
3) Situation 1
Le skieur remonte la piste à vitesse constante.
a. Construire sur un schéma la somme vectorielle des forces représentées.
Cette somme vectorielle se nomme la résultante des forces et se note ΣF.
b. Que vaut ΣF ? Que peut-on en déduire concernant les actions mécaniques s’exerçant sur le système ?
c. Ce système est-il pseudo-isolé ?
d. En déduire les caractéristiques du vecteur quantité de mouvement p du centre d’inertie du système.
4) Situation 2
Pendant une durée Δt très courte, certaines actions mécaniques s’exerçant sur le système sont modifiées. On
considère les forces modélisant ces actions, de valeur constante sur cette durée. La vitesse du système augmente
alors.
a. Quelles sont les deux forces représentées qui ont été modifiées par rapport à la situation 1 ?
b. Construire sur un schéma la somme vectorielle de ces forces. Quelles sont les caractéristiques de ΣF ?
c. Le système est-il pseudo-isolé ?
d. Le vecteur quantité de mouvement p2 a-t-il varié par rapport à p1 ? Donner les caractéristiques de
Δp = p2 - p1
POUR CONCLURE
5) Pendant la durée Δt, quelles sont les caractéristiques communes à ΣF et Δp ?