Régime transitoire équation différentielle

Etudes des circuits linéaires en régime transitoire
Page 1 sur 11
17/04/2017
M.M.
Régime transitoire équation différentielle.
I/ Régime permanent – Régime transitoire.
1) Régime permanent :
On s’est placé jusqu'à présent en régime permanent : la tension ou le courant du circuit de
[ ; ] t
.
Exemple : régime sinusoïdal.
2) Régime transitoire :
En réalité il existe une période de « mise en route » au moment ou l’utilisateur allume le
générateur, courant et tension vont évoluer avant d’atteindre le régime permanent. Cette phase
correspond au régime transitoire.
Plus généralement, il existe un régime transitoire entre deux régimes permanents.
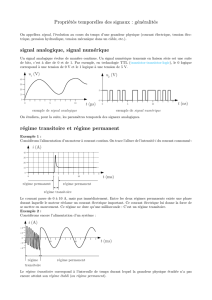
Exemple :
Régime permanent
Régime transitoire

Etudes des circuits linéaires en régime transitoire
Page 2 sur 11
17/04/2017
M.M.
L’étude du régime transitoire d’un circuit permet de déterminer de nombreuses
caractéristiques de ce circuit.
II/ Circuit électrique de premier ordre.
1) Rappel :
Résistance :
Condensateur :
Remarque :
C
ti
dttdu )()( 
C est différent de zéro, donc
dttdu )(
ne peut pas être infinie.
u(t)
i(t)
C
dttdu
Cti
dqtdq
ti
C
tq
tu )(
.)(
)(
)(
)(
)(
t
u(t)
Régime
permanent
sinusoïdal
Régime
transitoire
u(t)
i(t)
R
)(.)( tiRtu 

Etudes des circuits linéaires en régime transitoire
Page 3 sur 11
17/04/2017
M.M.
Par conséquent la tension aux bornes d’un condensateur varie de façon continue.
Inductance :
Remarque :
L
tu
dttdi )()( 
L est différent de zéro, donc
dttdi )(
ne peut pas être infinie.
L’intensité du courant traversant une inductance varie de façon continue.
2) Circuit du premier ordre :
Circuit n°1 :
Maille du circuit :
)()()()()( tutRitutute CCR 
Or
dttdi
Cti )( )( 
On a donc :
)(
)(
)( tu
dttdu
RCte C
RC
te
tu
RCdt tdu C
C)(
)(
1
)( 
L
u(t)
i(t)
dttdi
Ltu )( .)( 
Cas impossible
(saut de tension)
i(t)
uC(t)
uR(t)
C
R
e(t)

Etudes des circuits linéaires en régime transitoire
Page 4 sur 11
17/04/2017
M.M.
Circuit n°2 :
On a :
dttdi
Ltututute RLR )( )()()()( 
Or
)(.)( tiRtuR
dt tdu Rdttdi R)(
.
1)( 
On a donc :
dt tdu R
L
tute R
R)(
.)()( 
R
L
te
tu
R
L
dt tdu R
R)(
)(
1
)( 
Un circuit électrique du premier ordre est un circuit dont les variations de tension aux bornes
d’un composant vérifient une équation différentielle linéaire du premier ordre.
Remarque :
Il existe des circuits de deuxième ordre (pas au programme).
3) Méthode de résolution d’une équation différentielle du premier ordre :
Les deux équations différentielles en 2) sont de la forme :
)(
1
)(
1)( tytx
dttdx
L
R
)(tuR
)(tuL
e(t)
i(t)

Etudes des circuits linéaires en régime transitoire
Page 5 sur 11
17/04/2017
M.M.
Remarque :
- t est homogène à un temps (seconde).
- y(t) dépend du type de génération utilisé
carré
sinus
continu
La solution générale de cette équation s’écrit :
)()()( 21 txtxtx 
Avec x1(t) solution de l’équation sans second membre (ESSM) :
0)(
1
)( 1
1 tx
dttdx
Et x2(t) solution particulière de l’équation qui dépend de la nature de y(t).
Cherchons l’expression de x1(t) :
0)(
1
)( 1
1 tx
dttdx
(ESSM)
)()( 11 tx
dttdx 
dt
tx tdx  )( )(
1
1
dt
tx tdx )( )(
1
1
2
1
11 )(ln K
t
Ktx 
3
1
1)(ln K
t
tx 
(K3 = K2 – K1)
3
1
)(
1
K
t
etx 