3 Vitesse et mouveme..

Chap 3 : VITESSE ET MOUVEMENT 1ère S
I] Rappels.
1) Référentiels et repères.
Le corps solide, par rapport auquel on étudie le mouvement d'autres corps, est appelé référentiel . (T, G, H = Copernic).
Pour repérer + facilement la position d'1 objet dans 1 , on définit 1 repère = système d'axes lié au référentiel (immobile / ).
2) Trajectoire.
La trajectoire d'1 point mobile dans un est la ligne constituée par l'ensemble des positions successives qu'il occupe au cours du t.
Elle dépend du d'étude.
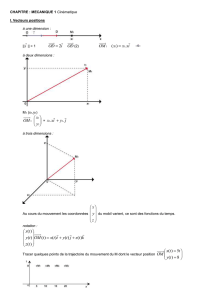
3) Repérage d'un point.
Un point M dans un plan est repéré à tout instant par ses coordonnées (x, y).
4) Solides et systèmes matériels.
Un système matériel est un objet (ou groupe d'objets) que l'on sépare arbitrairement de son environnement pour l'étudier.
5) Point matériel.
Un objet peut être assimilé à un point matériel si ses dimensions sont négligeables à l'échelle du problème à résoudre.
II] Centre d'inertie d'un solide.
toujours 1 pt du solide dont le mvt est + simple que les autres. Ce point est le centre d'inertie
G du solide.
Lorsque le solide est homogène et de forme géométrique simple, G est confondu avec le centre
géométrique.
III] Vitesse d'un point mobile.
1) Vitesse moyenne. Vmoyenne = / pour un point mobile longueur parcourue en m. durée du trajet en s, V en m.s-1.
2) Vitesse instantanée.
La vitesse instantanée V(t2) d'un point mobile à l'instant t2 est égale à sa vitesse moyenne
calculée entre deux dates t1 et t3 aussi rapprochées que possible de la date t2 :
V(t2) = M1M3 / t3 – t1
On peut confondre la longueur de l'arc M1M3 avec celle du segment [M1M3] si l'intervalle de
temps t3 – t1 est très petit.
Si Vinstantanée = cte, le mouvement est dit uniforme, sinon il est varié.
3) Vecteur vitesse.
La connaissance de la vitesse instantanée d'un mobile ne suffit pas à savoir où il se trouvera l'instant d'après. Il est nécessaire de
définir un vecteur vitesse :
A l'instant t, le vecteur vitesse v(t) d'un point mobile M a pour caractéristiques :
Point d'application : la position qu'occupait M mobile à t.
Direction : celle de la tangente à la trajectoire au point occupé par M mobile à l'instant t (voir schéma précédent),
Sens : celui du mouvement à l'instant t,
Norme : valeur de la vitesse instantanée à l'instant t.
4) Coordonnées et composantes du vecteur vitesse.
La connaissance d'un vecteur passe souvent par celle de ses coordonnées dans le repère choisi.
v(t) = vx(t) + vy(t) = vx(t) i + vy(t) j. Par projection orthogonale du vecteur vitesse sur les 2 axes du
repère, on obtient ses composantes.
Si on définit un angle : vx(t) = V(t) cos et vy(t) = V(t) sin
IV] Etude de quelques mouvements d'un point mobile.
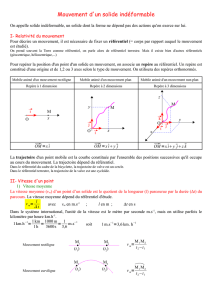
1) Mouvement rectiligne uniforme.
Les positions successives du point M sont alignées : le mouvement est rectiligne ( circulaire ou curviligne). Schéma.
Elles sont régulièrement espacées et le mobile va tjs dans le même sens: le mouvement est uniforme ( varié).
V(t2)

Si le mouvement est rectiligne uniforme, le vecteur vitesse est constant (même direction, sens et norme).
2) Mouvement circulaire.
Lorsque le mouvement est circulaire et uniforme, la direction du vecteur vitesse est
portée par la tangente au cercle au point considéré. Cette direction change lorsque M se
déplace sur sa trajectoire. Le vecteur vitesse n'est donc pas constant, seule son intensité
l'est.
Comment déterminer la valeur de la vitesse instantanée ? Ici : V = / t = .R / (12t).
V] Etude de quelques mouvements d'un solide non ponctuel.
1) Mouvement de translation rectiligne.
Tous les points d'un solide en translation ont, à chaque instant, le même vecteur vitesse v(t) et chaque segment du solide reste // à lui-
même au cours du déplacement. On distingue 2 cas :
Les trajectoires des points du solide sont des droites : le solide est animé d'un mouvement de translation rectiligne.
Les trajectoires des points du solide sont des courbes superposables : il est animé d'un mouvement de translation curviligne.
2) Mouvement de rotation autour d'un axe fixe .
Au cours de la rotation d'un CD, deux rayons tournent du même angle durant le même intervalle de temps. On dit qu'ils tournent
avec la même vitesse angulaire .
La vitesse angulaire d'un solide mobile autour d'un axe fixe est donnée par la relation : = / . Unités : rad, s, rad . s-1.
Relation entre v et :
Un point M situé à R de l'axe de rotation décrit durant l'intervalle de temps un arc de cercle
de longueur : = .R.V = / = R / = R = V.
Mouvement de rotation uniforme :
Il s'agit d'un mouvement périodique. La période T du mouvement est égale à la durée d'un tour : T = 2 /. Unités : s, rad,
rad.s-1. La fréquence f du mouvement est égale à l'inverse de la période. f = 1/T. f en Hz. On peut aussi écrite = 2f.
1
/
2
100%