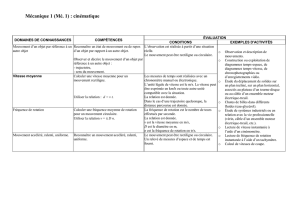
vitesse point -et -moyenne

CHAPITRE : MECANIQUE 1 Cinématique
I. Vecteurs positions
à une dimension :
||
i
|| = 1
iOD  2
OD
(2)
1OM
ixxx  .)( 11 
à deux dimensions :
M1 (x1,y1)
1OM
1
1
y
x
=
ixx  .1
jy  .1
à trois dimensions :
Au cours du mouvement les coordonnées
z
y
x
du mobil varient, ce sont des fonctions du temps.
notation :
ktzjtyitxtOM
tz
ty
tx 
 )()()()(
)(
)(
)(
Tracer quelques points de la trajectoire du mouvement du M dont le vecteur position
8)(
5)(
ty
ttx
OM

II. Vecteur vitesse (instantanée)
Cas général :
dt
OMd
v
v
vttOMttOM
v
tOMOM
v
OMOMOMMOMM
t
m
lim
)()(
'
'''
0
k
dt
dz
j
dt
dy
i
dt
dx
v
vz
dt
dz
vy
dt
dy
vx
dt
dx
v
k
dt
dz
j
dt
dy
dt
di
xi
dt
dx
v
dtkzd dtjyd dtixd
v
kzjyix
dt
d
v
z
y
x
)()()(
)(
exemple :
Déterminer les coordonnées du vecteur vitesse instantanée de l’exemple du I.
1
1
.0
.5
8)(
5)(
smv
smv
v
ty
ttx
OM
y
x
On donne le vecteur vitesse d’un point M dans le repère
),;( jiO 
tv
smv
vy
x
10
.5 1
Déterminer les coordonnées du vecteur position. Le point M se trouve à l’origine du repère à t = 0
'²5)(
)(
ktty
ktx
OM
à t = 0
'0)0(
0)0(
ky
kx

III. Vecteur accélération
0:
0
)()(
.lim
)()'(
0
dt
vd
donc
cstva
t
dt
vd
ta
dt
vd
a
aa ttvtv
a
tmoyenne
moyenne
Si le mouvement est rectiligne uniforme alors le vecteur accélération est nul
Nature d’un mouvement :
- mouvement rectiligne uniforme
droite
vitesse constante
- mouvement rectiligne accéléré
droite
vitesse augmente
- mouvement rectiligne décéléré / ralenti
droite
vitesse diminue
- mouvement circulaire uniforme
cercle
vitesse constante
- mouvement circulaire accéléré
cercle
vitesse augmente
- mouvement circulaire ralenti
cercle
vitesse diminue
- mouvement parabolique :
/
/

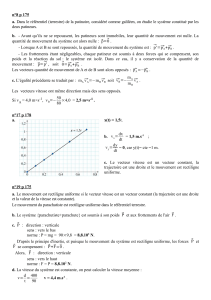
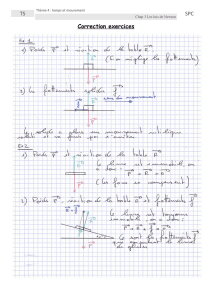
Exercice
1.Calculer les coordonnées de
a
de l’exemple I.
2.Déterminer les coordonnées du vecteur position du point M dont
a
est donné par
5
0
a
1.
1
1
.0
.5
8)(
5)(
smv
smv
v
ty
ttx
OM
y
x
0
0
y
x
a
a
a
dt
v
a
dt
v
a
dt
v
a
a
z
z
y
y
x
x
remarque :
²
²
dt
OMd
dt
OMd
dt
d
dt
vd
a
2.
²
2
5
0
'²
2
5
5
0
5
0
'5
5
ty
x
v
kty
kx
v
t
v
tv
v
v
ktv
v
v
y
x
y
x