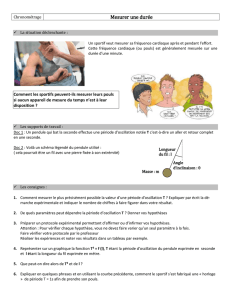
E 6 : Prendre max 10° et l = constante ( entre 50 et 80 cm )

1
TP P 5 : Le Pendule Pesant
1. Rappel des formules du pendule pesant (pendule simple)
C 1 : Période :
g
l
2T 
si max est petit
)
16
1(
g
l
2T 2
max
si max est grand
( max est exprimé en radians )
C 2 : Equation horaire :
max
)
Tt2
sin( 
si max est petit
C 3 : Energie cinétique :
22
K)
dt
d
(ml
2
1
E
C 4 : Energie potentielle :
)cos1(mglEP
avec
0EP
pour  = 0 (c'est à dire à l'équilibre )
C 5 : Energie mécanique :
KPm EEE 
2. Influence de m, l, θmax sur la période T d’un pendule
simple:mise en évidence expérimentale.
2.1. Relation entre T et m.
E 6 : Prendre max  10° et l = constante ( entre 50 et 80 cm )
Faire varier la masse m , et mesurer à chaque fois 10 périodes T .
m ( g )
20
40
60
80
100
T ( s )
1,5
1,5
1,5
1,5
1,5
E 7 : Tracer T = f ( m ) à l’aide de REGRESSI

2
Par un défaut technique (nous avions un chronomètre mécanique et non électronique), nos mesures de T
sont très approximatives.
On remarque que la période est constante quelle que soit la masse m, la période est invariante :
la durée de la période est indépendante de la masse m.
2.2. Relation entre T et l.
E 8 : Prendre m = 50 g (ou une autre masse) et max  10°.
Faire varier l , et mesurer à chaque fois 10 périodes T .
l ( cm )
20
40
60
80
100
T ( s )
9,5
12,5
15
18
20
T2 ( s2 )
90,25
156,3
225
324
400
E 9 : Tracer T = h( l ) et modéliser en utilisant le modèle « puissance » de REGRESSI.
Q 10 : En déduire l’intérêt de tracer la « courbe » T² = f( l) pour pouvoir faire une exploitation graphique
simple .

3
On obtient à peu près une courbe proche de T=h(l)=a* l0.5 avec a=2s; aussi, en traçant la courbe T² = f( l),
on peut récupérer une droite d’équation T² = a² * l, ce qui simplifiera l’exploitation graphique.
E 11 : Tracer T 2 = f (l ) par REGRESSI
La courbe obtenue est une droite. Le carré de la période est proportionnel à la longueur l du
pendule.
E 12 : Remarque : méthode "dynamique " pour mesurer l'intensité de la pesanteur au lieu considéré.
On a :
gl4
T2
2
La pente p (ou coefficient directeur ) de la courbe T 2 = f ( l ) a pour valeur :
g
4
p2
, d'où :
p
4
g2
.
Retrouver la valeur de g à partir de celle de p.
Suite de Q 10 , en posant (p=a²) : Sur la courbe expérimentale, on a p = 3,99 s2.m -1
D’où : g = 9,89 m.s-2 cette valeur est proche de la valeur de référence g0= 9,81 m.s -2 .
Conclusion : la méthode expérimentale du pendule pesant, par la mesure des périodes au carré T²
par rapport à la longueur du pendule permet de retrouver l’intensité de la pesanteur en un point
de la surface terrestre, en l’occurrence le laboratoire.
2.3. Relation entre T et θmax .
E 13 : Prendre m = 100 g et l = constante (entre 50 et 80 cm) : l = 60cm
E 14 : Faire varier l’amplitude angulaire max, et mesurer à chaque fois 10 périodes T, et remplir le
tableau ci –après :
max (°)
3
5
10
15
20
30
40
50
60
max (rad)
π/60
π/36
π/18
π/12
π/9
π/6
9π/2
18π/5
π/3
max2 (rad2)
(π/60)²
(π/36)²
(π/18)²
(π/12)²
(π/9)²
(π/6)²
(2π/9)²
(5π/18)²
(π/3)²
T (s)
1.575
1.572
1 .594
1.588
1.585
1.615
1.625
1.650
1 .669

4
E 15 : En traçant T = f( θ) et en modélisant sous la forme T = A +(B* θn), on obtient une courbe de très
bonne approximation ( écart relatif : 0,64% ; a=1.54s ; b=0.114 s ; n=0.5)
E 16 : Aussi en traçant T= f (max2), on simplifie l’exploitation graphique car on a une droite affine .
E 17 : On peut modéliser la courbe par la relation : T = Q (1+ k. max2) (écart relatif seulement 0.44%).
E 18 : Déterminer Q et k . Conclure.
On détermine expérimentalement : Q=1,58s
k= 0.54
Or étant donné que pour θ en radian petit, par exemple θ≤π/12, max2 est d’autant plus petit (ordre de
grandeur de moins de 10-2) ; de plus 0≤k ≤1; donc la valeur de Q.k. max2 est dans ce cas très négligeable.
Conclusion : la longueur du fil du pendule étant constante, pour θ très petit, on peut approximer :
T ≈ Q.
Aussi, pour θ très petit, pour l donné, la valeur de la période du système oscillant peut être
considéré comme constante.
3. Etude des oscillations d'un pendule simple à l'aide d'un
logiciciel d'acquisition.
On utilise le logiciel Synchronie 2003 couplé avec une interface d'acquisition directe:
EUROSMART associée au dispositif Pendulor. On va ainsi pouvoir suivre directement la variable

5
associée au pendule pesant (l'angle α = θ) au cours du temps.
3.1. Réalisation des enregistrements
3.1.1. Mise en route du logiciel et réglage du zéro:
E.19 : Sur le bureau, ouvrir Synchronie 2003, la fenêtre d'acquisition par Synchronie 2003 apparaît.
E.20: Cliquer sur l'onglet paramètres. La fenêtre des paramètres d'acquisition s'affiche.
E 21 : Sélectionner l'onglet entrées et vérifier que l'entrée EAO est en configuration automatique et est
affichée dans la fenêtre 1.
E.22 : Cliquer sur l'onglet acquisition et fixer une durée de 2.5s pour un total de points de 1000
(pour les deux derniers enregistrements, il faudra fixer la durée à 12 s et le nombre de points à 5000).
E.23: En laissant le pendule à sa position d'équilibre, lancer une acquisition en appuyant sur F 10.
Pendant cette acquisition, tourner le disque situé sur l'axe de rotation du pendule pour se placer à 0,00 V.
E.24 : Une fois le réglage précédent effectué,lancer une nouvelle acquisition en appuyant sur F 10 en
maintenant le pendule à 90,0° de sa position d'équilibre ( on pourra utiliser une équerre et un fil à
plomb).
E 25 : Après cette acquisition, relever la valeur de la tension constante mesurée à l'aide de l'onglet
réticule. Noter cette valeur: V1=6 ,06V.
3.1.2. Mode opératoire pour enregistrer les oscillations.
E 26 : Mesurer la distance 1 de l'axe de rotation au centre de masse du cylindre pesant fixé en bout de
tige, ainsi que la masse m de ce cylindre.
l = 0,465 m m = 0,142 kg
E.27 : Ecarter le pendule pesant de sa position d'équilibre. E 28 : Le lâcher sans vitesse initiale.
E 29 : Déclencher l'enregistrement en tapant sur F 10.
3.1.3. Mode opératoire pour sauvegarder les enregistrements :
E.30. Cliquer sur Fichier / enregistrer sous et sauvegarder sur disquette ou clé USB au format texte:
osci1.TXT (ou txt) après avoir indiqué les variables à enregistrer : T le temps et EA0 : la tension v1
E 31 : Sur le bureau, cliquer sur l'onglet Regressi. La fenêtre bien connue de Regressi s'affiche. Cliquer
alors sur fichier /ouvrir et aller chercher le fichier texte sauvegardé précédemment. Les données
acquises s'affichent alors regroupées dans un tableau donnant T et EAO.
E 32 : Modifier, le nom de T en t (pour ne pas faire de confusion avec la période du mouvement).
E 33 : Créer la variable α à partir de EAO. Pour cela, créer une nouvelle variable calculée α =
90*EA0/(V1) en remplaçant V1 par la valeur déterminée précédemment en E 25E.34. : Cliquer sur
Fichier / enregistrer sous. Choisir ensuite un nom de fichier : oscill.rw3 et la disquette ou la clé USB
comme destination.
3.2. Enregistrements.
3.2.1. Faible amplitude, frottement négligeable
E 35 : Noté oscfafn1 (2.5 s de durée)
3.2.2. Grande amplitude, frottement négligeable
E.36 : Noté oscgafn2 (2.5 s de durée)
3.2.3. Faible amplitude, avec frottement fluide
E 37 : Noté oscfaff3 (ne pas oublier de changer la durée à 12 s)
3.2.4. Faible amplitude, avec frottement solide
E.38 : Noté oscfafs4 (ne pas oublier de changer la durée à 12 s)