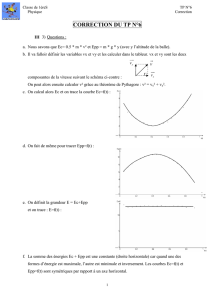
Correction de l`exercice 24 p 272 On cherche la vitesse initiale à

Correction de l'exercice 24 p 272
On cherche la vitesse initiale à donner à la fusée pour qu'elle arrive à une hauteur h = 15 m avec une vitesse nulle.
Pour cela, comme on peut négliger les frottements, on va utiliser (comme dans quasiment tous
ces exercices) la conservation de l'énergie mécanique.
Pour clarifier les choses, prenons l'origine des altitudes au point A, où on lance la fusée.
Au point A :
Em(A) = Ec(A) + Ep(A) = 
 où K est une constante, en Joules.
Au point B,
Em(B) = Ec(B) + Ep(B) = 
Du fait de la conservation de l'énergie mécanique, on obtient que Em(A) = Em(B)
D'où   
D'où   
D'où 
AN :
 (on vérifie que h est bien exprimé en m !)
  (On ne garde que 2 chiffres significatifs ici car h n'est exprimé qu'avec 2 CS)
Reste à convertir cette vitesse en km/h :
Correction de l'exercice 31 p 272
1. a -  
Comme OA = L,  
De même,  
Comme OB = L,  
b - L'énergie potentielle en A vaut
Epp (A) = mgzA + K = - mgLcos(αA) + K
où m est la masse du pendule en kg et g l'intensité du champ de pesanteur.

Reste à déterminer K.
Dans l'énoncé, il est écrit que par convention, on prendra ici Epp (O) = 0 J.
Si on prend l'origine de l'axe des z en O, on obtient donc que K = 0 J.
D'où Epp (A) = - mgLcos(αA)
De même, Epp (B) = - mgLcos(αB)
Attention à bien vérifier que l'énergie potentielle d'une masse m est plus faible si celle ci est située en A plutôt
qu'en O !
2. a- Au point A :
Au point B :
Comme en B, la vitesse de la masse est nulle, l'énergie cinétique est nulle.
On a donc
b- Pour trouver l'amplitude angulaire maximale αB du mouvement du pendule, on utilise la conservation de
l'énergie mécanique. Cette grandeur est en effet conservée puisque dans l'énoncé, il est précisé que les
frottements sont ici négligeables.
On a donc :
D'où, en utilisant les réponses de la question 2-a :
On a donc :
Ou encore
AN :
Attention à bien mettre les distances en m et les vitesses en m/s pour l'application numérique !
L'écartement angulaire maximal du pendule est de 52°.