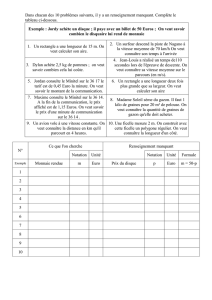
NARRATION DE RECHERCHE

RECHERCHE DU PROBLEME DE CARRELAGE avec CYRIL
- La longueur et la largeur ne sont pas connues, est ce qu’il faut les inventer pour faire ce problème ?
- Sûrement qu’il vaut mieux commencer par des petits nombres pour les dimensions du rectangle.
- Les nombres seront entiers, il est impossible qu’il y ait des nombres décimaux car, dans l’énoncé on
dit : la longueur et la largeur du rectangle sont des multiples entiers des dimensions du carreau unité de
un sur deux.
- On remarque que si on prend un rectangle de 3 sur 4, le produit de la longueur par la largeur est pair.
- Pour trouver le nombre de carreaux, il faut diviser par deux, car le carreau unité occupe deux places
carrées de un sur un.
On peut mettre 6 carreaux dans le rectangle
Par exemple comme ça :
- Mais si on prend d’autres dimensions pour le rectangle et que le produit n’est pas un nombre pair, il y
aura des trous. Exemple avec 3 sur 5
On peux mettre 7 Carreaux dans le rectangle, mais il restera un trou
- On remarque qu’il y aura donc plusieurs réponses mais qu’avec les cas où « largeur multiplié par
longueur égale un nombre pair »
- Donc la réponse est « oui » mais il y aura beaucoup de réponses; On pense même qu’il y en aura à
l’infini.
- C’est sur qu’en multipliant la longueur par la largeur, il faudra obligatoirement trouver un nombre
pair sinon il y aura des trous.
A Partir de cette observation qui a fait consensus dans la classe :
« En multipliant la longueur par la largeur, il faudra obligatoirement trouver un nombre pair sinon il y
aura des trous, et ce ne sera pas possible de carreler »
Beaucoup de stratégies par dénombrement, des façons possibles de placer les carreaux, sur des
dessins avec diverses dimensions du rectangle à carreler.
- Rectangle de 1 sur 2 : une seule possibilité de placer le carreau unité
- Rectangle de 2 sur 2 : il faudra 2 carreaux, et deux possibilités de placer ces deux carreaux
- Rectangle de 2 sur 3 : il faudra 3 carreaux, et trois possibilités de placer ces trois carreaux
- Rectangle de 2 sur 4 : il faudra 4 carreaux, et cinq possibilités de placer ces trois carreaux
- …….
On va peut être trouver une relation entre le nombre de carreaux et le nombre de façons de carreler,
sans être obligé de faire plein de dessins comme exemples ?
Et, en plus que c’est fatiguant, est ce que ça suffit comme preuve de compter sur des dessins ?
X