24 janvier 2005

24 janvier 2005
Réponses aux questions
3ème3 de Saint-Mathieu
Que veut dire « multiple entier d’une même unité de longueur » ?
Cela veut dire que les dimensions du rectangles sont un nombre entier d’une unité qu’on a choisie.
Quelle est l’unité de longueur ?
Groupe 1 :
m² et cm
Groupe 2 :
le cm
Groupe 4 et groupe 6 :
des mètres
Groupe 5 :
l’unité de longueur est de 2.
Groupe 7 :
on ne la connaît pas elle est la même pour m et n.
Quand on dit largeur 1 et longueur 2 cela signifie que la longueur est le double de la largeur ?
Oui pour les groupes 1, 3, 4 et 5.
Non pour les autres : car c’est comme A et B ; 1 et 2 sont des noms pour définir les 2 largeurs.
Combien mesurent les côtés de la forme rectangulaire ?
Groupe 1 :
on ne sait pas
Groupe 2 :
elle mesure m et n.
Groupe 3 :
quelle forme rectangulaire ?
Groupe 4 :
(n+m)x2
Groupe 5 :
largeur 1, longueur 2
Groupe 7 :
ils mesurent m et n
Quelle est la mesure des carreaux ?
Groupe 1 et groupe 5 :
1 de largeur et 2 de longueur.
Groupe 2 :
1x2
Groupe 3 :
la longueur est le double de la largeur qui est un nombre quelconque.
Combien mesure la surface à carreler ?
Groupe 1 :
on ne sait pas
Groupe 2 :
mxn
Groupe 3 :
on ne sait pas mais la longueur et la largeur sont différentes.
Groupe 4 :
mxn
Groupe 5 :
la surface à carreler est égale à m et n.
Groupe 7 :
on ne la connaît pas ( m x n ) .
Est-il possible de carreler une forme rectangulaire avec des multiples différents ?
Groupes 1, 5 et 6 : oui
Groupe 2 :
si on coupe les carreaux.
Groupe 3 :
ça veut dire quoi ?
Groupes 4 et 7 :
non.
Y a-t-il une aire à calculer ? Si oui, laquelle ?
Groupes 1, 2, 3, 4, 6 et 7 : oui, celle du rectangle, m x n.
Groupe 5 :
non.
Faut-il calculer le périmètre ?
Groupes 1, 4, 5 et 7 :
oui.
Groupes 2 et 3 :
non
Groupe 6 :
pas forcément.
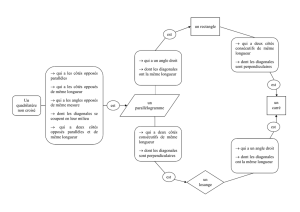
Quelles sont les propriétés du rectangle ?
Groupe 1 :
diagonales de même longueur,
côtés opposés parallèles et de même longueur.
Groupe 3 :
côtés opposés parallèles et égaux.
Groupe 4 et groupe 5 :
il a 4 angles droits, les côtés parallèles 2 à 2 et les diagonales se coupent en leur
milieu, les côtés opposés égaux.
Groupe 6 :
4 angles à 90°, côté opposé parallèle
Groupe 7 :
les côtés opposés sont // et il a 4 angles droits et c’est un parallélogramme et les diagonales se
coupent en leur milieu.
Est-ce possible d’obtenir un rectangle avec la largeur et la longueur égales à 2 ?
Est-ce qu’un carré est un rectangle ?
Tout les groupes ont répondu oui à ces deux questions car un carré est un rectangle particulier.
Est-ce que les carreaux sont rectangles ?
Tout les groupes ont répondu oui.
Est-il utile de trouver à quels chiffres correspondent m et n ?
Oui pour tous sauf le groupe 5 qui pense que ce n’est pas utile.
Peut-on résoudre le problème sans ces chiffres ?
Groupes 1, 2 ,4 et 5 :
non
Groupes 3 et 6 :
oui
Groupe 7 :
oui et non ; si on n’a pas les chiffres, le nombre de solutions est infini.
Quel théorème faut-il utiliser pour cette résolution ?
Groupes 1, 3 et 6 :
théorème de Pythagore
Groupes 2, 4, 5 et 7 :
aucun théorème