Correction du devoir n°1 de mathématiques

1 Bac 4 octobre 2006
Ph. Georges Maths
DEVOIR DE MATHÉMATIQUES
I- Résoudre dans I; R les équations suivantes sans utiliser la méthode du discriminant.
1) (x – 4) (x + 3) = 0 4) x 2 – 25 = 0
2) (x + 5) (x – 6) (2x – 8) = 0 5) x 2 – 6x + 9 = 0
3) x 2 – 9x = 0
II- Recopier la réponse choisie (une seule réponse exacte).
1) Les nombres 1 et 3 sont solutions de
l'équation :
x 2 – 2x + 1 = 0
Error! – 2x +
Error! = 0
x 2 – 12x + 27 = 0
2) Les solutions de l'équation
x 2 + 2x + 1 sont :
x1 = – 1 ; x2 = 0
x0 = – 1
x1 = 1 ; x2 = 0
3) Les solutions de l'équation
x 2 – 8x + 3 = 0 sont les abscisses des
points d'intersection de la parabole y = x 2
et de la droite d'équation :
y = – 8x + 3
y = 8x – 3
y = 8x + 3
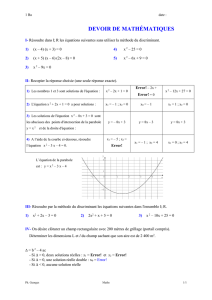
4) La courbe ci-dessous a pour équation
y = x 2 – 3 x – 4.
En déduire les solution de l'équation :
x 2 – 3 x – 4 = 0
x1 = – 5 ; x2 =
Error!
x1 = – 1 ; x2 = 4
x1 = 0 ; x2 = 4
III- Résoudre par la méthode du discriminant les équations suivantes dans l'ensemble I; R.
1) x2 + 2x – 3 = 0 2) 2x2 + x + 5 = 0 3) x 2 – 10x + 25 = 0
IV- On désire clôturer un champ rectangulaire avec 200 mètres de grillage (portail compris).
Déterminer les dimensions L et l du champ sachant que son aire est de 2 400 m2.
x
y
-1
0
1
2
3
4
-5
5
1

1 Bac 4 octobre 2006
Ph. Georges Maths
Correction du devoir n°1 de mathématiques
I- Résoudre dans I;R les équations suivantes sans utiliser la méthode du discriminant.
1) (x – 4) (x + 3) = 0 «Un produit de facteurs est nul si l'un des facteurs est nul.»
On résout les deux équations du premier degré : x – 4 = 0 et x + 3 = 0.
On obtient : x = 4 et x = – 3 S = { –3 ; 4 }
2) (x + 5) (x – 6) (2x – 8) = 0 «Un produit de …» d'où les équations : x + 5 = 0 ;
x – 6 = 0 ; 2x – 8 = 0. On obtient : x = – 5 ; x = 6 et x = 4 S = { – 5 ; 4 ; 6 }
3) x2 – 9x = 0 est équivalente à x (x – 9) = 0 «Un produit de …»
d'où les équations : x = 0 et x – 9 = 0 On obtient : x = 0 et x = 9 S = { 0 ; 9 }
4) x 2 – 25 = 0 est équivalente à x2 – 52 = 0. On reconnaît l'identité remarquable a2 – b2 = (a – b) (a + b).
(x – 5) (x + 5) = 0 «Un produit de …» d'où les équations : x – 5 = 0 et x + 5 = 0
On obtient les solutions : x = 5 et x = – 5. S = { – 5 ; 5 }
5) x 2 – 6x + 9 = 0 On reconnaît l'identité remarquable a2 – 2ab + b2 = (a – b)2.
La factorisation permet d'écrire : (x – 3) 2 = 0«Un produit de …»
d'où l'équation : x – 3 = 0. La solution double est x = 3 S = { 3 }
II- Recopier la réponse choisie (une seule réponse exacte).
1) Les nombres 1 et 3 sont solutions de l'équation
Error!
– 2x +
Error!
= 0.
2) La solution de l'équation x 2 + 2x + 1 est : x0 = – 1.
3) Les solutions de l'équation x 2 – 8x + 3 = 0 sont les abscisses des points d'intersection de la
parabole d'équation y = x 2 et de la droite d'équation y = 8x – 3.
4) Les solutions de l'équation x 2 – 3 x – 4 = 0 sont : x1 = – 1 et x2 = 4.
III- Résoudre par le calcul les équations suivantes dans l'ensemble I;R.
1) x2 + 2x – 3 = 0
On calcule le discriminant   = (2)2 – 4 (1) (– 3)  = 16  > 0
L'équation admet 2 solutions x1 =
12
162
x2 =
12
162
S = { – 3 ; 1 }
2) 2x2 + x + 5 = 0
On calcule le discriminant   = (1)2 – 4 (2) (5)  = – 39  < 0
L'équation n'admet pas de solution dans I; R. S = 
3) x 2 – 10x + 25 = 0 On reconnaît l'identité remarquable a2 – 2ab + b2 = (a – b)2
d'où : (x – 5) 2 = 0 «Un produit de …» S = { 5 }
IV- On désire clôturer un champ rectangulaire avec 200 mètres de grillage (portail compris).
Déterminer les dimensions du champ sachant que son aire est de 2 400 m2.
L2 – 100 L + 2400 = 0 Les solutions sont : L' = 40 et L" = 60
L' = 40 donne l' = 60 qui est une solution à rejeter car l L.
Le champ a 60 m de longueur et 40 m de largeur.