GENERALITES SUR LES FONCTIONS

GENERALITES SUR LES FONCTIONS
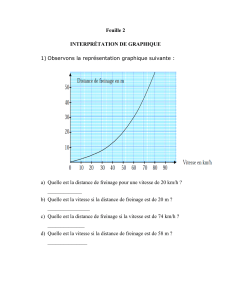
ACTIVITÉ 1 :
a) sur quel intervalle de temps se fait l'étude ci-dessus ? (on appelle cet intervalle l'ensemble
de définition)
b) pour t=5 heures, quel est le taux d'alcoolémie ? (cette valeur est appelée l'image de
l'abscisse t=5)
c) à quels moments atteint-on une alcoolémie de 1g/L ? (ces deux valeurs sont 2
"antécédents" de l'ordonnée A=1)
d) donner les coordonnées du point représentant l'alcoolémie maximale atteinte
e) comment varie le taux d'alcoolémie en fonction du temps ?
Pour un homme de 80 kg ayant absorbé environ 4
verres de vin.
Il y a une correspondance entre le temps qui
s'écoule et la variation du taux d'alcoolémie.
Cette courbe est une fonction représentant le taux
d'alcoolémie en fonction du temps.
Document à lire

GENERALITES SUR LES FONCTIONS
OBJECTIFS : -
-
-
-
-
I- VOCABULAIRE:
Mes loisirs "sont fonction" ( ou dépendent) du temps qu'il fait.
Le périmètre du cercle (
R 2
) est " fonction"(dépend) de la longueur du rayon du cercle.
Le terme "est fonction de" signifie qu'une grandeur dépend d'une autre, d'où le terme de fonction f qui dépend
de x.
II- DEFINITIONS ET ACTIVITÉ :
Y
C
P
P
y
=f (
P
x
)
a O
P
x
b
III- DÉFINITION:
La correspondance d'un ensemble de valeurs de [a ; b] vers un ensemble de valeurs de [c ; d] est une fonction
si, à un élément x de [a ; b], on associe un seul et unique élément de [c ; d].
On note f : [a ; b] [c ; d]
x y = f(x)
Exemple: n'est pas la courbe représentative d'une fonction car
…………………………………………………………….
…………………………………………………………….
Celle-ci est bien la représentation graphique d'une fonction
(Oy) est l'axe des
………………
….
C est la ………………
……………………….
(Ox) est l'axe des
………………
….
P
y
est ………………..
f(
P
x
) est
l'……………….
………………
……………….
P
x
est l' ………
ou l' …………..
de f(
P
x
)
[a ; b] est l'ensemble
………………………

Applications : 1- Soit la fonction définie par f(x) = 2x²-x-4
a) Remplir le tableau de valeurs
x
-2
-1
0
1
2
3
f(x)
b) tracer la courbe représentative de cette fonction
2- Soit f(x) = x²-6x +8
a) Calculer f(2), f(2,5), f(3), f(3,5), f(4).
b) Tracer la courbe dans un repère orthonormé
OBJECTIFS N°1 ET 2 A REMPLIR

IV- SENS DE VARIATION :
1- DÉFINITION:
Une fonction f est croissante sur un intervalle I si pour tous réels
1
x
et
2
x
de I,
21 xx 
entraîne
)()( 21 xfxf 
f(
2
x
)
f(
1
x
)
1
x
2
x
Une fonction f est décroissante sur un intervalle I si pour tous réels
etx1
2
x
de I,
21 xx 
entraîne
)()( 21 xfxf 
f(
1
x
)
f(
2
x
)
1
x
2
x
en français : f est croissante : plus x grandit, plus f(x) grandit
f est décroissante : plus x grandit, plus f(x) est petit
2- EXEMPLE:
1 f est croissante sur [….;…..]
f est décroissante sur [……;…….]
-3 4
1
remarque : La fonction peut être constante sur un intervalle :
1
x
2
x
entraîne f(
1
x
)=f(
2
x
)
3- APPLICATION:
La fonction f est croissante et f(2) = 0
Déduire si f(0) est positif ou négatif
Le taux d'alcoolémie est …………………… sur l'intervalle [0 ; 1]
Le taux d'alcoolémie est ……………………… sur l'intervalle […..;…..]
f est constante

V- TABLEAU DE VARIATION :
1- structure:
f est croissante sur [a ; b]
x
a b
f(x)
f(b)
f(a)
f est décroissante sur [a ; b]
x
a b
f(x)
f(a)
f(b)
2- exemple numérique :
2
1
-3 -2 -1 0 1 5
f est croissante sur ……………puis sur………….
f est décroissante sur ………………
3- Méthode:
 Déterminer les intervalles de la variable x sur lesquels f est croissante ou décroissante
 Placer dans le tableau les bornes de ces intervalles par ordre croissant
 Indiquer par des flèches les sens de variations de f
 Noter les valeurs images f(x), des bornes x
4- Application: f est définie sur [0,5 ; 4] par
x
xf 1 )( 
a) compléter le tableau
x
0,5
1
2
3
4
f(x)
b) tracer la courbe de f
c) construire le tableau de variation de la fonction f.
x
0 1 8
f(x)
1,2
0 0
Ceci est le tableau de variation de la fonction représentant les variations
du taux d'alcoolémie en fonction du temps.
Sur [0 ; 1] f est croissante et est compris entre 0 et 1,2.
Sur [1 ; 8] f est décroissante et est compris entre 1,2 et 0.
x
f(x)