Exercice 1 : ABC est un triangle équilatéral, M, N, P sont des points

A
B
C
D
N
M
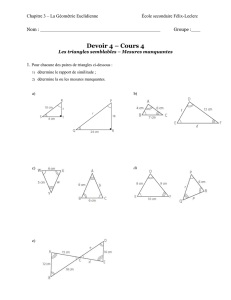
Exercice 1 : ABC est un triangle équilatéral, M, N, P sont des points de
[BC], [CA], [AB] tels que BM = CN = AP.
1. Démontrer que les triangles BMP, CNM et NAP sont isométriques
deux à deux.
ABC equilateral: BC = AC = AB et
60A B C  
°
Par hypothèse: BM = CN = AP,
Par soustraction : MC = AN = PB,
Donc : BMP, CNM et NAP sont isométriques (cas n°3 : 2 cotes egaux chacun à chacun et
l’angle formé par les 2 cotés)
2. En déduire que MNP est équilatéral.
Déduction : les 3° cotes sont égaux chacun à chacun : PM = MN = NP
Donc : MNP est équilatéral
Exercice 2 : ABCD est un carré, (DM) est tangente au cercle C de diamètre [AB].
1. Démontrer que les triangles OAD et OMD sont isométriques.
90AOD OMD
° (angle du carré & tangente)
OD est cote commun
OA = OM = rayon
Dans un triangle rectangle, si je connais 2 cotés, je peux calculer le 3°.
2 2 2 2
AD OD AO MD OD MO    
= côté du carré(*)
Donc : les triangles OAD et OMD sont isométriques (cas n°1 : les 3 cotes égaux chacun à
chacun)
2. Démontrer que les triangles DMR et DCR sont isométriques.
90RCD RMD
° (angle du carré & tangente)
On a (question ci-dessus) : MD = côté du carré(*)= DC
DR est cote commun
Meme raisonnement que ci-dessus : les 2 triangles rectangles ont 2 cotés egaux chacun a
chacun : donc le 3° cote est egal chacun a chacun : MR = CR
Les triangles DMR et DCR sont isométriques (cas n°1 : les 3 cotes égaux chacun à chacun)
3. En déduire la nature du triangle CMR.
Ci-dessus on a montré que MR = CR, alors CMR est isocele en R
Exercice 3 : ABCD est un parallélogramme, N un point du segment [DC] distinct de D et C.
La droite (AN) coupe (BC) en M.
1. Démontrer que les triangles ADN et ABM sont des triangles semblables.
ADN ABM
(Angles opposés dans le parallélogramme)
DAN AMB
(Angles alternes-internes : (AD)//(BM)
ADN et ABM sont des triangles semblables cas n°1 : ayant
2 angles egaux chaun a chacun
2. En déduire que DN  BM = AB  AD.
Dans 2 triangles semblables, les cotes opposes aux angles
égaux sont proportionnels :
AD DN AN
MB BA MA
; le produit en croix donne la réponse
2
1
2
2
1
2
1
1

Exercice 4 : Sur la figure ci-dessous, ABC est un triangle, H le projeté orthogonal de A sur
[BC],
BAH
= 45°,
HAC
= 30° et AH = 6 cm.
Le cercle C de diamètre [AH] et de centre O coupe (AB) en D et (AC) en E.
1. montrer que les triangles AHC et AEH sont semblables
AHC est rectangle avec un angle de 30° ; l’autre angle mesure alors 60°.
AHE est inscrit dans le cercle avec [AH] diametre –
donc : AHE est rectangle avec le meme angle de 30° ; donc le 3° angle de
60°
les triangles AHC et AEH sont semblables (cas n°1 : les 3 angles egaux
chacun a chacun)
2. Montrer que AC =
43
cm
AHC est rectangle avec l’angle
HAC 
30° :
cos( ) cos(30 ) AH HAC AC
;
36
2AC
Produit en croix : AC =
12 12 3 43
3
3
3. Montrer que AE = 3 3 cm.
AHE est rectangle avec l’ angle
HAC 
30° :
cos( ) cos(30 ) AE HAE AH
;
3
26
AE
Produit en croix : AE =
63 33
2
4. déduire le rapport de réduction pour passer de AHC à AEH
AHC et AEH ont les cotes (en face des angles egaux) proportionnels :
3 3 3
62
AE
AH 
; C’est le rapport de réduction
(En bonus pour les élèves qui aiment les maths)
5. montrer que AB =
62
(valeur exacte)
Dans AHB rectangle en H :
cos( ) cos(45 ) AH HAB AB
;
26
2AB
Produit en croix : AB =
12 12 2 62
2
2
6. Démontrer que
AHE
=
ADE
= 60°
AHE
=
ADE
car ils interceptent le meme arc
AE
Or :
AHE
= 60° (car l’autre angle du triangle rectangle AHE mesure 30°)
donc :
AHE
=
ADE
= 60°
7. Démontrer que BAC et EAD sont semblables.
75BAC DAE
° (angle commun)
2
1
1
1
1

AHE
=
ADE
= 60°(démontré ci-dessus)
Donc le 3° angle est égal chacun a chacun : BAC et EAD sont semblables (cas n°1)
8. En déduire que
6
4
est le rapport de réduction qui fait passer du triangle BAC à EAD.
BAC et EAD son semblables alors ils ont les côtés (en face des angles égaux) proportionnels :
3 3 3 6
4
6 2 2 2
AE
AB   
; C’est le rapport de réduction