Pour une sémantique de la dénomination et de la

Pour une sémantique de la dénomination et de la référence
Pierre Frath
Département d'anglais
UFR des Langues Vivantes
EA 1339 Linguistique et didactique des langues
Université Marc Bloch
22 rue Descartes
67084 Strasbourg
France
Email : [email protected]
Le 20e siècle n'a pas fait une grande place à la référence en linguistique. Pourtant, sans la
notion que nous utilisons les mots pour parler de notre expérience, l'étude du sens perd une
grande partie de son intérêt. Il se conçoit alors, selon les théories, au sein d'un logicisme
universalisant, comme des interactions dans des systèmes de signes, ou encore comme des
corrélations autistiques entre signes et concepts. Dans tous les cas, rien n'est dit sur le moteur
de l'activité linguistique, à savoir notre désir de parler de notre expérience
1
.
Dans cet article, nous passons rapidement en revue la référence telle qu'elle est perçue par les
approches du sens les plus marquantes du 20e siècle, à savoir la philosophie du langage, le
structuralisme et le cognitivisme. Nous posons ensuite la notion de dénomination à partir de la
sémantique référentielle de Georges Kleiber et celle de signe interprétant à partir de la
sémiotique de C. S. Peirce. Nous proposons enfin une conception de la référence dont nous
illustrons l'intérêt à l'aide de quelques exemples.
1. Référence et philosophie du langage
La référence est une notion ancienne en philosophie. Aristote distingue la référence des noms
propres, qui désignent selon lui une substance unique comme le ciel, le soleil, la lune, Platon,
Parménide, etc. et la référence des adjectifs (blanc, beau, rond,…) ou des noms de classe
(chien, arbre, …), qui désignent des universaux. Que les mots réfèrent est ainsi admis comme
une évidence, le problème pour Aristote étant d'expliquer pourquoi certains mots parviennent
à référer à des catégories, alors que d'autres ne réfèrent qu'à des objets uniques. Il ramène le
premier de ces modes de référence au second en constatant que la blancheur, la beauté, la
rondeur, etc. ne peuvent exister qu'à travers des objets qui possèdent la caractéristique d'être
blancs, beaux ou ronds. Les universaux n'ont ainsi de réalité que par l'intermédiaire de la
substance. Ces deux modes de référence sont recouverts par une distinction métaphysique
fondamentale établie par Aristote entre la matière et la forme. La forme est un idéal qui peut
s'incarner de nombreuses fois dans la matière. Par exemple, lorsque l'artisan fabrique des
boules de bronze, il utilise une forme existante idéale (la sphère) qu'il applique à de la matière
(le bronze).
1
Sur les nécessités de changements dans la théorie linguistique, voir aussi l'article de Jean-Pierre Durafour dans
ce volume.

Il y aurait donc une sorte d'isomorphie universelle entre les mots et leurs référents matériels et
idéels, dont les relations réciproques seront l'objet de toutes les théories philosophiques
analytiques jusqu'à nos jours. Par exemple, Bertrand Russell, un défenseur d'une vision du
monde empiriste, exprime ainsi les relations entre les choses, les qualités et les mots : "Let us
give the name "qualities" to specific shades of colour, specific degrees of hardness, sounds
completely defined as to pitch and loudness and every other distinguishable characteristic,
and so on. [...] Common sense regards a "thing" as having qualities, but not as defined by
them. [...] I wish to suggest that, wherever there is, for common sense, a "thing" having the
quality C, we should say, instead, that C itself exists in that place, and that the "thing" is to be
replaced by the collection of qualities existing in the place in question." (1950, p. 98).
Une chose est donc composée de qualités, que l'on peut nommer, et les mots et les choses se
superposent sans problème à chaque étape de l'analyse, jusqu'aux constituants matériels
ultimes. Ainsi, les mots étant capables, idéalement, de représenter les choses, les relations
entre ces dernières peuvent être étudiées en utilisant les mots à leur place dans des énoncés
obéissant à certaines normes logiques. La logique est ainsi dotée d'une valeur universelle
capable de décrire à la fois les choses, nos idées sur les choses, et le langage que nous
utilisons. Il était dès lors tentant de ramener les mathématiques à la logique, ce que Russell et
Whitehead d'une part et Hilbert d'autre part ont essayé de faire, les premiers dans leurs
Principia mathematica en 1910, 1912 et 1913, le second dans ses Grundlagen der
Mathematik en 1934 et 1939. Goedel sonne le glas de ces tentatives avec son théorème
d'incomplétude
2
en 1931, dans lequel il montre que la vérité d'une proposition au sein d'une
axiomatique ne peut pas toujours être assertée. Comme il est impossible de parvenir à la vérité
à partir de l'intérieur d'un système, il ne peut y avoir de logique universelle qui comprendrait
tous les systèmes, car la vérité nécessite un point de vue extérieur, qui ferait alors défaut.
Beaucoup d'auteurs ont introduit explicitement la pensée dans le couple mot v. référent. Nous
n'en donnerons que deux exemples, G. Frege et Ogden & Richards. Le premier a abordé le
rapport entre le concept, le sens et l'objet d'une manière originale à la fin du 19e siècle, et ses
travaux conservent toute leur pertinence aujourd'hui. Pour lui, "il est naturel d'associer à un
signe (nom, groupe de mots, caractères), outre ce qu'il désigne et qu'on pourrait appeler sa
dénotation, ce que je voudrais appeler le sens du signe, où est contenu le mode de donation
de l'objet. ... La dénotation d'"étoile du soir" et d'"étoile du matin" [est] la même, mais leur
sens [est] différent (Frege 1892, 1971 : 103). Frege distingue donc l'objet dénoté, qui peut être
"donné" de plusieurs manières, du sens, qui en est le "mode de donation". Ce sens est souvent
interprété comme étant l'ensemble des "idées" que nous avons sur l'objet, c'est-à-dire un ou
plusieurs concepts. Pourtant, Frege fait une autre distinction, celle d'une représentation
distincte du sens. "La dénotation d'un nom propre est l'objet même que nous désignons par ce
nom; la représentation que nous y joignons est entièrement subjective; entre les deux gît le
sens, qui n'est pas subjectif comme l'est la représentation, mais qui n'est pas non plus l'objet
lui-même" (Frege 1892, 1971 : 106). Il distingue clairement un sens public, lié aux signes, et
un sens privé, fait des impressions personnelles de chacun. Il illustre cela ainsi : "Chez le
même individu, la même représentation n'est pas toujours liée au même sens. Car la
représentation est subjective ; celle de l'un n'est pas celle de l'autre. Et il est bien naturel que
les représentations associées au même sens diffèrent grandement entre elles. Un peintre, un
cavalier et un naturaliste lieront sans doute des représentations bien différentes au nom
"Bucéphale". C'est par là qu'une représentation se distingue essentiellement du sens d'un
signe. Celui-ci peut être la propriété commune de plusieurs individus : il n'est donc pas partie
2
"On formally undecidable propositions of Principia Mathematica and related systems",
http://www.ddc.net/ygg/etext/godel/godel3.htm.

ou mode de l'âme individuelle. Car on ne pourra pas nier que l'humanité possède un trésor
commun de pensées qui se transmet d'une génération à l'autre" (Frege 1892, 1971 : 105-
106).
Pour Frege, donc, les objets nous sont "donnés" de diverses manières par la langue en tant
qu'elle est un système de signes collectif, ce qui nous permet d'acquérir des connaissances sur
ces objets. En outre, le résultat de cette activité produit en nous des impressions et des
représentations psychologiques qui nous sont particulières.
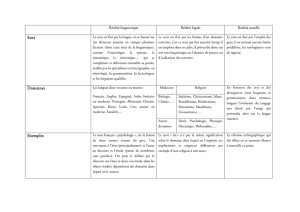
Ogden et Richards (1923) prennent une toute autre direction. Ces auteurs sont à l'origine du
célèbre triangle sémiotique que nous reproduisons ci-dessous dans son état originel.
Pour Ogden & Richards, la pensée équivaut à la référence et constitue le lien entre les mots et
les objets. En effet, selon eux, il ne peut y avoir de lien direct entre le signe et la chose, ce lien
ne pouvant s'établir que par l'intermédiaire de la pensée, qui réfère, c'est-à-dire qui met en
relation le symbole et le référent. Ils expriment cela ainsi : "Between the symbol and the
referent there is no relevant relation other than the indirect one, which consists in its being
used by someone to stand for a referent. Symbol and Referent, that is to say, are not
connected directly […] but only indirectly round the two sides of the triangle." (Ogden &
Richards 1923: 9-12).
La tradition analytique donne ainsi toute sa place à l'objet dans sa relation avec les mots et la
pensée. Cependant, les multiples théories en présence ne permettent pas de se faire facilement
une idée précise de l'importance relative qu'elles accordent à ces trois constituants. Qui plus
est, les distinctions opérées par les différents auteurs ne se recouvrent pas forcément. En
outre, des tentatives de simplifications ont donné lieu à l'élimination de l'un des trois sommets
du triangle. Ainsi, Bertrand Russell s'est-il fait l'avocat, contre Frege, d'une conception du

langage qui élimine le sens linguistique comme mode de donation de l'objet : le sens des mots
est dans les objets qu'ils désignent (une conception contre laquelle Ogden & Richards se sont
inscrits en faux).
Les linguistes n'ont pas été en reste en ce qui concerne les tentatives de simplification. On
peut dire que les travaux de Frege et d'Ogden et Richards illustrent les deux voies principales
utilisées pour l'élimination de la référence en linguistique. Frege pose effectivement la langue
comme un système de signes qu'il est tentant d'étudier en soi, comme l'ont fait les
structuralistes ; quant à Ogden & Richards, l'accent mis sur la pensée en tant que mécanisme
de mise en relation annonce les conceptions cognitivistes de la langue comme construction
régulée de systèmes de représentations mentales.
2. Référence et structuralisme
Le structuralisme écarte explicitement la référence de ses préoccupations. Dans son article sur
"La nature du signe linguistique", Benveniste (1966 : 49-62) examine la définition du signe
donnée par Saussure dans son "Cours de Linguistique générale" (1972 : 99) et qu'il résume
ainsi : "le total résultant de l'association d'un signifiant (=image acoustique) et d'un signifié
(=concept)" (Benveniste 1966 : 49). Saussure ajoute que "le signe unit non une chose et un
nom, mais un concept et une image acoustique" (Saussure 1972 : 98). Cette définition est
devenue classique et elle a abouti à ce que l'on appelle la "clôture linguistique". La langue
étant considérée comme un système de signes, il convient de l'étudier en tant que tel sans faire
intervenir des notions extérieures au système, telles que les choses et la pensée. Benveniste
note que ce "problème métaphysique de l'accord entre l'esprit et le monde [est un] problème
que le linguiste sera peut-être un jour en mesure d'aborder avec fruit, mais qu'il fera mieux
pour l'instant de délaisser" (Benveniste 1966 : 52)
3
.
Et en effet, nombre de linguistes rejettent la prise en compte de l'objet réel dans l'étude du
sens. Greimas par exemple la juge "impraticable" et même "onirique" : "toute recherche
portant sur les significations inhérentes à une langue naturelle reste enfermée dans ce cadre
linguistique, et ne peut aboutir qu'à des expressions, formulations ou définitions présentées
dans une langue naturelle. La reconnaissance de la clôture de l'univers sémantique
implique, à son tour, le rejet des conceptions linguistiques qui définissent la signification
comme la relation entre les signes et les choses, et notamment d'accepter la dimension
supplémentaire du référent.... Car se référer aux choses pour l'explication des signes ne veut
rien dire de plus que tenter une transposition, impraticable, des significations contenues dans
les langues naturelles en ensembles signifiants non-linguistiques : entreprise, on le voit, de
caractère onirique" (Greimas 1986 : 15-16),
Il y a des raisons historiques à cette position. La clôture a permis à la linguistique de se
constituer en une discipline distincte de disciplines voisines comme la philosophie et la
psychologie. Pour Saussure, la langue est forme, et non substance. L'étude de la substance
doit être laissée provisoirement à d'autres disciplines, tandis que la linguistique doit se
consacrer à l'étude des formes. C'est également la position de Bloomfield (1933, 1970 : 35) :
"Par suite de la répartition du travail scientifique, le linguiste ne s'intéresse qu'au signal
linguistique ; il n'est pas compétent pour traiter des problèmes de physiologie ou de
3
Descartes a abordé cette question dans ses Méditations métaphysiques. Il met la justesse de la correspondance
entre le concept et l'objet sur le compte d'un Dieu qui ne trompe pas les hommes et qui a fait en sorte que ce que
je conçois corresponde bien à ce que je perçois..

psychologie". Cette position a permis à la linguistique de se développer et de produire un
corps de connaissances considérable sur la langue et le langage.
Toutefois, la définition saussurienne du signe n'est pas aussi cohérente qu'il y paraît.
Benveniste, pourtant un disciple éminent du grand linguiste genevois, note que pour ce
dernier, "la nature du signe est arbitraire parce qu'il n’a avec le signifié 'aucune attache
naturelle dans la réalité'. Il est clair que le raisonnement est faussé par le recours inconscient
et subreptice à un troisième terme, qui n'était pas compris dans la définition initiale. Ce
troisième terme est la chose même, la réalité. Saussure a beau dire que l'idée de 'sœur' n'est
pas liée au signifiant de /sœr/ ; il n'en pense pas moins à la réalité de la notion. Quand il
parle de la différence entre /bœf/ et /oks/, il se réfère malgré lui au fait que ces deux termes
s'appliquent à la même réalité. Voici donc la chose, exclue expressément d'abord de la
définition du signe, qui s'y introduit par un détour et qui y installe en permanence la
contradiction. Car si l'on pose en principe – et avec raison – que la langue est forme, et non
substance, il faut admettre – et Saussure l'a affirmé nettement – que la linguistique est science
des formes exclusivement. D'autant plus impérieuse est alors la nécessité de laisser la
'substance' sœur ou bœuf hors de la compréhension du signe. Or c'est seulement si l'on pense
à l'animal 'bœuf' dans sa particularité concrète et 'substantielle' que l'on est fondé à juger
'arbitraire' la relation entre /bœf/ d'une part, et /oks/ de l'autre, à une même réalité. Il y a
donc contradiction entre la manière dont Saussure définit le signe linguistique et la nature
fondamentale qu'il lui attribue" (Benveniste 1966 : 50). Benveniste met cette "anomalie dans
le raisonnement" sur le compte d'un déterminisme philosophique de la fin du 19e siècle, qui
ne sera pas développée ici (voir Benveniste 1966 : 50-51).
Ajoutons que, si la conception saussurienne du signe a été extrêmement productive, la clôture
linguistique a tout de même eu pour effet d'enfermer la langue dans une conception autistique
qui relie deux objets internes, le signifiant et le signifié, et qui rend impossible la prise en
compte du réel, le lien entre signe et référent devenant mystérieux. Pour Benveniste, "si le
sens de la phrase est l'idée qu'elle exprime, la référence de la phrase est l'état de choses qui
la provoque, la situation de discours ou de fait à laquelle elle se rapporte, et que nous
pouvons jamais, ni prévoir, ni deviner" (Benveniste 1974 : 226-227). Mais comment l'idée
exprimée dans la phrase pourrait-elle correspondre à un état de choses si certains des signes
que nous associons au sein de la phrase ne correspondent pas à des éléments de cet état de
choses ? Nous pourrions alors dire n'importe quoi à propos de n'importe quelle situation.
Il faut se résoudre à mettre l'"anomalie" sur le compte d'un état de fait : les signes sont bien
des pointeurs sur des objets, et Saussure s'est vu contraint de réintroduire subrepticement
l'objet dans son raisonnement après l'avoir d'abord éliminé.
3. Référence et cognitivisme
Pour les philosophes du langage, il est naturel de prendre en considération les trois sommets
du triangle sémiotique, même si les diverses théories s'intéressent plus à certains de ses côtés
qu'à d'autres. Les structuralistes, quant à eux, se sont explicitement interdit l'étude de la
référence, non parce qu'ils pensaient qu'elle n'est pas partie prenante de notre activité
linguistique, mais pour des raisons méthodologiques : il est plus simple, pour l'instant,
d'étudier la langue comme un système de signes, quitte à réintroduire le lien avec le monde
lorsque les bases auront été acquises. Les structuralistes n'ont donc pas nié l'importance du