Génétique des populations

Génétique des populations – Génétique évolutive
I) Introduction
C’est la discipline la plus concernée par les problèmes de société actuels. Pour commencer il
faut connaître quelques définitions :
- Gène : unité d’information biologique, transmise au cours des générations et codant pour
une fonction particulière. C’est une séquence d’une macromolécule (ADN ou ARN) transmise
telle quelle (à de rares modifications près), transcrite et généralement traduite, ce qui permet
l’expression d’une activité biologique (critères morphologiques, protéines…)
On change d’échelle par rapport à la génétique formelle, on s’intéresse à de grandes
populations avec un grand nombre de gènes (et aussi de nombreuses mutations).
- Locus : historiquement, position du gène sur le chromosome. En génétique des populations,
ensemble des gènes homologues (classe d’homologie). Deux chromosomes ou deux gènes
sont homologues s’ils s’apparient et s’excluent mutuellement à la méiose.
- Allèle : deux gènes homologues sont dits allèles quand ils ont des formes différentes,
distinguables à un niveau d’observation donné. Un allèle peut donc correspondre à une seule
séquence, ou à un ensemble de séquences différentes mais non distinguables au niveau du
phénotype. (ex : couleur des yeux bleu/marron/vert mais au niveau du nucléotide on a
beaucoup plus d’allèles différents, plusieurs par couleur).
1) Qu’est-ce que la génétique des populations, à quoi sert-elle ?
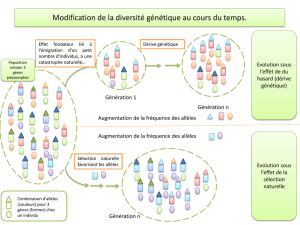
Basée sur l’existence d’une variabilité génétique (mesurable) et de l’hérédité, elle concerne de
nombreux gènes avec plusieurs allèles (couleur des yeux, isoenzymes, mutations
ponctuelles…), ou des changements dans la fréquence allélique (évolution des populations ou
des espèces).
Des erreurs lors de la transmission sont la source de variabilité permettant l’évolution. Ces
erreurs, faites par les polymérases, ne sont pas « négatives » puisqu’elles sont utiles à
l’évolution. On peut faire des probabilités et des estimations de fréquence pour prédire les
changements.
La génétique des populations mesure la variabilité génétique dans et entre des populations, et
retrace l’histoire évolutive des espèces : quantification et description. Elle explique les
modifications observées dans le temps et dans l’espace par les forces évolutives, donnant des
explications et des prédictions.
« Rien en biologie n’a de sens, si ce n’est à la lumière de l’évolution » Th. Dobzhansky
En systématique, on étudie la classification des êtres vivants. En physiologie, on étudie le
fonctionnement des êtres vivants. La théorie de l’évolution justifie et explique la mise en
place de fonctions (le hasard et la nécessité). La génétique des populations s’applique aussi à
la biologie moléculaire (évolution moléculaire)…
Les domaines d’application :
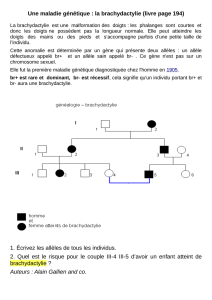
- Médecine et génétique humaine : épidémiologie des maladies génétiques (mutation et
sélection, 6000 connues chez l’homme), effets de la consanguinité, raison de l’augmentation
de la myopie, de la galactosémie…
- amélioration génétique animale et végétale : sélection artificielle. Le maïs dérive d’une
plante sauvage, la téosinthe (produisant seulement 2 ou 3 grains) et la sélection a permis
d’arriver à 200-300 grains.
- OGM : dissémination, impact sur l’écosystème.

Les problèmes d’espèces invasives, les réintroductions d’espèces, la conservation génétique,
la biodiversité font intervenir la génétique des populations.
Une population est un ensemble d’individus se reproduisant ensemble (à l’inverse, les espèces
sont des ensembles d’individus potentiellement interféconds). Ce sont donc des individus de
la même espèce qui ont la possibilité d’interagir entre eux au moment de la reproduction.
Une population est une unité évolutive, les gènes sont différents selon les populations. C’est
aussi une unité écologique, c’est un ensemble d’individus soumis aux mêmes pressions de
sélection.
Une population correspond à un pool génétique, un ensemble de génotypes individuels pour
chacun des gènes : A1/A2 B1/B2/B3. On peut alors introduire des notions statistiques.

Pour prévoir les proportions, on se sert des gamètes et de leur fréquence : la reproduction
correspond au tirage au sort de gamètes dans deux urnes de gamètes (paternels et maternels).
La génétique formelle s’intéresse à un génotype et aux gamètes, la génétique des populations
concerne un ensemble de génotypes (fréquence) et au pool de gamètes (ou urne, encore une
fréquence). La génétique des populations est donc probabiliste :
- grand nombre d’individus
- grand nombre de générations
- grand nombre de populations
- facteurs évolutifs multiples
Tout ceci fait qu’il y a une grande difficulté à expérimenter. Il faut donc utiliser des
simulations et des modélisations (et quelques calculs de probabilités).
2) Les théories de l’évolution
Une théorie scientifique se base sur des observations pour la formulation d’une hypothèse
(modèle). Celle-ci est rejetée ou améliorée à partir d’expérimentations. Il faut avoir un
principe de parcimonie, la théorie la plus simple est la meilleure.
La théorie de l’évolution sert à expliquer l’origine et la diversité des êtres vivants.
Il y a tout d’abord eu des théories de créationnisme et de fixisme :
- Carl von Linné (1707-1778) : la création unique
- Cuvier (1769 – 1832) : créations successives (cataclysmisme)
- Lamarck (1744 – 1829) : débuts du transformisme, hérédité des caractères acquis.
Depuis on sait que les mutations et les changements sont aléatoires, il n’y a pas de
transmission de caractères acquis aux descendants. Cependant, chez les virus, un état de stress
augmente le taux de mutation, et des radiations (ou autres mutagènes) peuvent intervenir :
l’environnement peut influer sur les caractères transmis.
- Darwin (1809-1882) : première théorie scientifique indiquant le rôle du milieu dans la
différenciation, et le rôle de l’isolement dans la spéciation. Il publie en 1859 « l’origine des
espèces » avec le concept de « struggle for life » (lutte pour l’existence), idée apportée par
Malthus. Celui-ci a été très important pour Darwin, il avait essayé de modéliser l’évolution
des populations et des ressources (qui sont limitées).
Les problèmes du Darwinisme étaient le support de l’hérédité et l’hérédité des caractères
acquis.
- Galton et les fondements de l’eugénisme (ex : 400 000 personnes stérilisées en Allemagne).
Galton tire les conséquences pratiques du Darwinisme
- Mendel (1865) : ses lois sont redécouvertes beaucoup plus tard, et permettent la naissance de
la génétique des populations. La théorie vient de JBS Haldane, RA Fisher, et S Wright.
L’expérimentation vient de L’Héritier et Teissier (« cages à populations »), ou de Ford (« la
génétique écologique »).
- Théorie synthétique de l’évolution (1937-1944) : Th. Dobzhansky, JS Huxley, E Mayr, GG
Simpson.
- Question centrale (1950-1960) : l’importance du polymorphisme dans les populations ?
Selon Müller, il y a élimination des allèles défavorables, mais Dobzhansky pense plutôt à un
polymorphisme équilibré. Le polymorphisme est en effet très élevé : d’où vient-il ? La théorie
neutraliste de l’évolution moléculaire et la phylogénie moléculaire permettent de donner des
réponses à cette question.
- Motoo Kimura (1968) : mutations dues au hasard, la sélection existe mais la plus grande
partie de la diversité est due au hasard par des mutations spontanées. On peut observer une
horloge moléculaire : l’apparition de modifications d’acides aminés est régulière au cours du

temps. Le pourcentage de substitution est proportionnel au temps de séparation des espèces, il
dépend de la taille du génome et du type de gènes.
- Actuellement : débat entre sélectionnistes et neutralistes : quelle importance pour chacun de
ces deux phénomènes ? Kimura et Crow ont travaillé sur le neutralisme. Le nouveau terrain
de bataille concerne les spéciations
Théorie synthétique de l’évolution :
- existence d’une variabilité
- hérédité des caractères
- sélection naturelle et hasard sont à l’origine de l’évolution des populations
3) La variabilité génétique
Les caractères sont variables, il n’y a pas deux individus semblables. Cette variabilité est
morphologique (peau…), chromosomique (nombre de chromosomes…), comportementale
(cour que font les oiseaux avec le chant), physiologique (résistance au froid, à la
sécheresse…), biochimique (protéines, enzymes) ou moléculaire (protéines, ADN). Les
différences peuvent être individuelles ou géographiques (races ou variétés) : microsatellites
(empreintes génétiques), couleur des vaches selon les régions, variétés de fleurs…
Il faut qu’un caractère soit codé par un gène et qu’il soit transmissible. On peut alors se
demander s’il y a un déterminisme génétique.
Variabilité v = vG + vE + vG-E (E pour environnement et G pour génétique)
Pour prouver le déterminisme génétique, il faut montrer qu’il s’agit d’un caractère héritable,
avec ségrégation mendélienne. Il existe des caractères qualitatifs (discrets) et quantitatifs
(poids).
On s’intéresse aux caractères à fort déterminisme génétique (ex : quantité de lait produite),
qu’ils soient qualitatifs (yeux : petit nombre de gènes, peu de caractères) ou quantitatifs
(poids dicté par 40 à 50 gènes, taille : grand nombre de gènes).
Variabilité épigénétique, plasticité phénotypique et mode de réaction :
Des individus à génotype identique peuvent avoir des phénotypes différents selon le milieu
(température…). Différents phénotypes sont possibles selon la « norme de réaction » (ex :
larve – adulte, castes, variation saisonnière, homochromie…). Il existe une variation
épigénétique due aux milieux instables : on peut citer par exemple le mourron rouge ou bleu
selon la nature du sol.
3 phénomènes sont la source de la variabilité génétique : ségrégation méiotique (2n types de
gamètes), recombinaisons et mutations (ponctuelles, remaniements chromosomiques).
Les mutations somatiques disparaissent avec l’individu, mais les mutations affectant les
gamètes sont transmises de génération en génération. La mutation est un phénomène aléatoire
et a un effet aléatoire sur les individus (favorable, neutre, délétère, létal).
On peut quantifier le degré de variabilité dans une population
Exemple chez les drosophiles : pour les gènes morphologiques on a 3 à 5 mutations par
individu à l’état hétérozygote, tout individu est porteur d’un allèle létal pour deux gènes en
moyenne.
Taux de polymorphisme P (proportion de gènes polymorphes parmi l’ensemble des gènes
étudiés) : P = nombre de gènes polymorphes / nombre total de gènes étudiés.

Un gène est dit polymorphe s’il existe au moins deux allèles, le plus fréquent ayant une
fréquence inférieure ou égale à 95% (ou 99%). Sinon on parle de cryptopolymorphisme.
Chez l’homme on a 30% de polymorphisme. Mais il y a un problème avec ce calcul : il ne
tient pas compte du nombre d’allèles (même valeur s’il y a 200 allèles différents ou seulement
2). Le polymorphisme augmente aussi avec la taille de l’échantillon : si on se limite à peu
d’individus (homme) la valeur trouvée sera inférieure à celle d’un grand échantillon
(bactéries) : problème statistique.
On se sert du taux d’hétérozygotie Ho : c’est la moyenne des fréquences d’hétérozygotes
observés pour chacun des loci.
Ho = Σ (Hi) x 1/N
(Avec Hi hétérozygotie au locus i, et N nombre de loci)
Chez l’homme, on arrive à Ho = 0,067 pour les loci enzymatiques (un individu est
hétérozygote pour 6,7% de ses gènes). On trouve une hétérozygotie plus importante chez les
invertébrés que chez les plantes, et encore moins importante chez les vertébrés. Les
hyménoptères ont une hétérozygotie inférieure à celle des autres insectes car les mâles sont
homozygotes (haploïdes, pas d’hétérozygotie possible puisqu’ils viennent de parthénogenèse)
et les gènes létaux s’expriment, ce qui diminue la variabilité.
Chez les espèces à effectif réduit, comme le guépard (P = 0,02 et Ho = 0,0004), la variabilité
diminue énormément (on peut faire des greffes de peau sans rejet). Ceci empêche la
reconnaissance du « soi », et provoque à terme la disparition de l’espèce. Une forte variabilité
permet à terme de s’adapter aux changements du milieu, mais au contraire il y a une plus forte
sensibilité aux parasites et aux pathogènes si les gènes d’histocompatibilité sont moins
variables.
Drosophile : enzymes groupe I P = 0,27 Ho = 0,04 très spécifiques
Enzymes groupe II P = 0,70 Ho = 0,24 peu spécifiques
Les enzymes à forte variabilité sont moins spécifiques, ce sont des enzymes « de ménage ».
La diversité génique est la probabilité de tirer deux allèles différents à un même locus en
tirant deux allèles au hasard dans la population : on l’estime par
2n (1 - Σ (pi²)) / (2n – 1)
n : nombre d’individus étudiés, pi : fréquence de l’allèle i dans la population
Ceci est valable quel que soit le degré de ploïdie et le mode de reproduction (ex : E. coli :
diversité = 0,5).
allèle
fréquence
1
P1
2
P2
3
P3
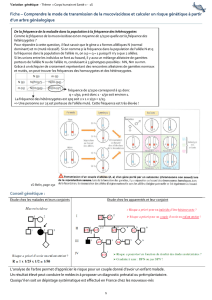
Le polymorphisme enzymatique chez la drosophile peut être étudié, par électrophorèse des
enzymes ADH et GDPH sur gel d’amidon. On révèle les protéines et on voit l’homozygotie
ou l’hétérozygotie.
FF  sous unité F  une bande
FS  sous unité F et S  2 bandes (si enzyme monomérique*)
SS  sous unité S  1 bande
*Si l’enzyme était dimérique, on aurait trois bandes correspondant aux associations possibles :
FF, FS et SS.
On peut calculer les fréquences de F et de S et prévoir leur évolution.