Student pour math

1
Jean François Kentzel – Lycée Pardailhan à Auch (32) – [email protected]
Soient
n
xxx ...
2,1
les résultats de n mesures indépendantes et suivant le même
protocole d’une quantité, désignée par m, dont on sait qu’elle est fixée. Intuitivement on
estime m par la moyenne empirique
nxx i/
. La LOI DES GRANDS NOMBRES permet
d’affirmer que cette estimation est d’autant meilleure que n est grand. On s’intéresse dans ce
qui suit (qui est la réponse à une question qui m’a été posée par une collègue de physique)
à la qualité de cette estimation lorsque l’entier n est fixé (n valant au moins 2).
Les calculs d’erreurs classiques, corrects mais parfois inopérants comme on va le voir plus
loin, sont à présent le plus souvent remplacés par des calculs probabilistes. Dans le cadre
probabiliste, effectuer une mesure c’est réaliser une expérience aléatoire, c’est à dire que le
résultat d’une mesure de la quantité m est donné par une variable aléatoire X. La définition
mathématique de ce qu’est une variable aléatoire importe peu ici, il suffit de penser que c’est
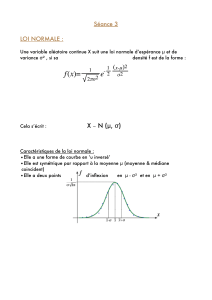
un nombre qui varie aléatoirement suivant une loi donnée. Le modèle courant est que X suit
une LOI NORMALE (dite aussi loi de Gauss ou plus familièrement « courbe en cloche »)
d’espérance (c’est à dire de moyenne) E ( X ) = m. On désigne par l’écart-type de la loi de
X. est une mesure de la dispersion des valeurs de X autour de sa moyenne m comme le
montre la définition de
2
( la variance de X ) : Var ( X ) =
2
= E ( X – m )2, c’est la
moyenne des carrés des écarts avec la moyenne.
On dit que X suit la loi N (
m
,
2
).
Sa densité, représentée ci-dessous, est f :
x
2
1
2
2
2
)( mx
e
.
Si ce modèle semble fantaisiste, on peut adopter le point de vue,
strictement équivalent, suivant lequel ce n’est plus le résultat
d’une mesure mais l’erreur effectuée sur une mesure qui est
aléatoire :
soit E la variable aléatoire « erreur commise sur une mesure ».
On a : X = m + E donc E = X – m suit la loi N(0,
2
).
Les dessins ci-contre montrent
les deux valeurs concernant la
loi normale N (
m
,
2
) qui
sont les plus utilisées.
Pour simplifier l’exposé, on
va, suivant l’usage, surtout
utiliser le dessin de droite. On
dira alors qu’on s’accorde une
marge d’erreur de 5 % .
LA LOI DE STUDENT ET LES MESURES SCIENTIFIQUES

2
On rappelle que ce dessin de droite signifie que si une variable aléatoire X suit N (
m
,
2
),
alors P (
22  mXm
) =
95.0)(
2
2
m
mduuf
: lorsqu’on effectue une mesure, on a
environ 95 % de chances pour que son résultat soit entre
2m
et
2m
1
.
Brève justification du modèle de la loi normale pour une mesure
Ce modèle ne heurte pas l’intuition : il suppose qu’on ne commet pas d’erreur systématique (symétrie autour de
la « vraie valeur m », les physiciens les plus pointilleux évitant d’utiliser cette expression et préférant parler de
valeur standard ou de valeur de référence) et que les petites erreurs sont plus fréquentes que les grandes
(concentration autour de m). Il est surtout confirmé, approximativement , bien sur, par un grand nombre
d’expériences. Un autre argument reposant sur le théorème dit de limite centrale va être donné dans ce qui suit2.
En cas de doute, on peut utiliser un test dit de normalité sur la série des mesures
n
xxx ...
2,1
. Un tel test,
indiquant si l’hypothèse que X suit une loi normale est raisonnable, est systématiquement effectué par un logiciel
évoqué plus loin.
La suite est une question de statistique tout à fait typique : que peut on
raisonnablement
3
dire de m à la seule vue des observations
n
xxx ...
2,1
?
Le dessin ci-contre illustre les règles :
E (X+Y) = E (X) + E (Y) (toujours vraie)
Var (X+Y) = Var (X) + Var (Y)
X+Y est normale si X et Y le sont
(vraies si X et Y sont indépendantes).
on peut déduire de ces règles que si les nombres aléatoires
4
n
xxx ...
2,1
suivent la loi N (m,
2
), alors le nombre (aléatoire)
n
ii
x
1
suit la loi N (n.m ; n
2
).
Par ailleurs en divisant une variable par un nombre a, on divise son espérance par a et sa
variance par a2 .On en déduit que
nxx i/
suit la loi N ( m,
n
2
). Ceci montre
5
que si on
a un écart-type pour une mesure, on a alors un écart-type
n
pour la moyenne de n
mesures.
On a donc une plus grande précision lorsqu’on calcule une moyenne de mesures.
C’est ici que les calculs d’erreurs classiques apparaissent comme inopérants. Ils donnent en effet, si on désigne
par e l’incertitude sur une mesure :
1
On dira plus loin que cette valeur 2 est en fait une valeur approchée de la valeur 1.96 mais pour l’instant ça n’a
aucune importance.
2
Ce théorème prouvant aussi qu’on peut s’affranchir de cette hypothèse de normalité dès qu’on prend un assez
grand nombre n de mesures, une borne courante étant n > 30.
3
en acceptant le modèle de la loi normale pour une mesure
4
Pour faciliter la communication avec les collègues de physique, on parle parfois de nombres aléatoires plutôt
que de variables aléatoires.
5
ça montre aussi à l’aide des règles rappelées que
n
mx
/
suit la loi N (0, 1). La forme de ce résultat incite à
noter ici un résultat difficile à prouver mais essentiel en calcul des probabilités : si X est une variable aléatoire
quelconque, de moyenne m et d’écart-type , ayant donné lieu aux valeurs observées
n
xxx ...
2,1
, avec n assez
grand (n > 30) alors le nombre aléatoire
n
mx
/
suit approximativement la loi N (0, 1). C’est le THEOREME DE
LIMITE CENTRALE. Il justifie ce qui a été écrit à la note 2, on peut se passer de l’hypothèse de normalité si n est
assez grand, et par ailleurs il donne une interprétation de cette hypothèse : l’erreur sur le résultat d’une mesure
pouvant être considéré comme la résultante d’un grand nombre de petites erreurs, dont les détails nous
échappent, il est raisonnable de considérer comme légitime que cette erreur suit une loi normale.

3
pour tout i, m – e
 i x
m + e d’où n(m – e)
i x
n(m + e) et m – e
 x
m + e.
Avec ces calculs, calculer une moyenne de mesures n’apporte aucune précision supplémentaire.
Puisque
x
suit la loi N ( m,
n
2
), on peut affirmer que
P (
n
mx
n
22 
) = P (
x
n
xm
n
22 
)
95.0
. (1)
Pour l’instant c’est seulement théorique puisque l’écart-type est inconnu.
Pour pouvoir en tirer des conséquences pratiques, on effectue alors une démarche courante en
statistique : estimer un paramètre inconnu à l’aide des observations dont on dispose :
De même qu’on avait estimé m par
nxx i/
qui est la moyenne de la série
n
xxx ...
2,1
des
observations, il est tentant d’estimer par s =
n
xxi
2
)(
puisque c’est l’écart-type de cette
série. Un petit calcul
6
(voir le paragraphe 5 de l’annexe) montre que le nombre s’ =
1nn
s
=
1
)( 2
n
xxi
, parfois dit écart-type débiaisé, est une meilleure estimation de .
Cependant la loi des grands nombres montre que cette estimation n’est correcte que si n est
assez grand; comme pour la borne n > 30 donnée précédemment (notes 2 et 3), suivant le
contexte et les auteurs on trouve aussi les bornes 20 ou 50.
On considère donc deux cas :
Premier cas : si n est assez grand, disons n > 30 : on remplace
n
par
n
s'
(ou par
1n
s
)
dans (1) : P (
x
n
s
xm
n
s'
2
'
2
)
95.0
. (2)
Puisqu’on dispose des nombres
x
et s’, (2) donne un encadrement de m avec une probabilité
de 0.95.
Comme on l’a vu précédemment (début de la note 3), dire que X suit la loi N (
m
,
2
) équivaut à dire
que
mX 
suit la loi N (0, 1). Or cette loi N (0, 1) est si importante qu’elle est tabulée, on peut donc modifier
le « taux de confiance de 95 % » pris dans tout ce qui précède en modifiant l’intervalle autour de
x
(et bien sur
plus le taux de confiance est grand, plus l’intervalle est grand). On peut par exemple affirmer avec la valeur 0.68
évoquée plus haut : P (
x
n
s
xm
n
s'' 
)
68.0
.
Deuxième cas : si n est entre 2 et 30
On dispose d’un résultat étonnant
7
pour qui croit que la statistique ne peut être utilisée que
lorsqu’on dispose d’un grand nombre d’observations : si X suit la loi N (
m
,
2
), alors,
6
On vérifie facilement que E (s’2) vaut
2
ce qui n’est pas le cas de E (s2).
7
résultat démontré au début du vingtième siècle, donc beaucoup plus récent que les autres qui sont évoqués dans
ce texte.

4
quelles que soient les valeurs de m et , le nombre aléatoire
t
=
ns
mx
/'
suit une loi fixée
8
et
connue, cette loi est appelée la loi de Student à (n-1) degrés de liberté
9
.
Désignant par Tn la loi de
Student à n degrés de
liberté, on donne ci-contre
la représentation graphique
des densités de T1, T2, T4 et
N (0 ; 1) sur [
4
; 4].
Quand n grandit, s’ se
rapproche de
et, voir le
début de la note 3, Tn se
rapproche de N (0 ; 1)10.
Au voisinage de 0, c’est la courbe normale qui est au dessus des autres.
Les expressions des densités des lois de Student sont assez compliquées et il n’est pas
question de prouver ici ce qui précède. On se contentera de l’illustrer avec un exemple simple.
L’important pour nos questions de mesures est que, comme la loi normale, les lois de Student
sont tabulées. Le tableau suivant, relatif au « taux de confiance » 95 %, peut être obtenu avec
=LOI.STUDENT.INVERSE(0,05;A1) tapé sur un tableur :
n
1
2
3
4
5
6
7
8
9
10
16
20
30
50
100
500
t 0.95; n
12,71
4,30
3,18
2,78
2,57
2,45
2,36
2,31
2,26
2,23
2,12
2,09
2,04
2,01
1,98
1,96
La signification du coefficient t 0.95; n est donnée par P (
t
< t 0.95; n )
95.0
pour
t
suivant la loi de Student à n degrés de liberté, ce qui donne, puisqu’on dispose de n mesures :
P (
ns
mx
/'
< t 0.95; n-1 )
95.0
, soit :
P (
1;95.0
'
n t
n
s
x
< m <
1;95.0
'
n t
n
s
x
) 0.95.
Comme en (2) ci-dessus, puisqu’on dispose des nombres
x
, s’ et t 0.95; n-1, on a un
encadrement de m avec une probabilité de 0.95.
Attention ! Dans tous les textes de physique figurant dans les références, le coefficient t 0.95; n-1
de ces formules est noté t 0.95; n et dans le tableau ci-dessus n désigne le nombre de mesures.
Cette notation, contraire à l’usage en statistique, est la cause d’au moins deux erreurs (voir
l’annexe) dont une, malheureusement, dans un programme de tableur par ailleurs bien
expliqué et très pratique.
Illustration :
On fait mesurer la longueur d’un objet (disons à un millimètre près et en utilisant seulement
un double-décimètre gradué en mm pour augmenter la variabilité des mesures) par un certain
nombre de personnes.
On peut simuler cette expérience : si l’objet mesure environ 10 mètres, chaque
personne va utiliser environ 50 fois la règle et un modèle de l’erreur (en mm) qu’elle va
8
notamment : cette loi ne dépend pas de m ni de .
9
n-1 car il y a une relation de dépendance entre les n variables dont les carrés figurent dans s’ :
)( xxi
= 0.
10
par exemple la valeur 1.96 intervenant dans le tableau ci-dessous est celle qui a été évoquée pour la loi
normale à la note 1. Dès que n est assez grand la loi de Student à n degrés de liberté est très bien approximée par
la loi normale N (0 ;1). En pratique, c’est à dire sur le plan des calculs, le premier cas (n > 30) est un cas
particulier du deuxième (n < 30).

5
commettre est
50
1ii
X
où les
i
X
sont 1[-0.5 ; 0.5] (nombre au hasard entre – 0.5 et 0.5, c’est la
formule =ALEA()
5.0
sur un tableur).
1 ) On vérifie d’abord en passant que l’hypothèse que les mesures
suivent une loi normale est raisonnable. On ne représente pas les
mesures obtenues mais seulement les erreurs, c’est à dire
50
1ii
X
. Les
histogrammes obtenus (en simulant 200 fois l’expérience) grâce à un
bon logiciel de regroupement en classes (voir l’annexe) sont
effectivement approximativement gaussiens.
2 ) L’objectif est en réalité de vérifier la loi de Student. On
demande donc à chacune des 200 personnes d’effectuer trois
mesures et de calculer
t
=
ns
x
/'
(la moyenne m des erreurs
valant 0). Pour 3 mesures le coefficient intéressant est t 0.95; 2 qui
vaut environ 4.3. Des appuis répétés sur la touche F9 donnent
bien comme ci-contre une dizaine de valeurs, soit 5 % de ces
valeurs, à l’extérieur de l’intervalle [
3.4;3.4
].
On peut également vérifier l’allure de la densité de T2 avec
l’histogramme obtenu pour la variable
t
.
Voir l’annexe (lisible sur la page http://pedagogie.ac-toulouse.fr/lyc-pardailhan-auch/, cliquer
sur ENT puis sur Rubriques des disciplines/ Mathématiques/ Documents- enseignants) pour
plus de détails sur certains points, une bibliographie contenant une vingtaine d’adresses
Internet et des références de logiciels rendant aisée l’utilisation de la loi de Student.
0
5
10
15
20
25
30
-6_-5,49
-4,97_-4,46
-3,95_-3,43
-2,92_-2,4
-1,89_-1,37
-0,86_-0,34
0,17_0,69
1,2_1,72
2,23_2,75
3,26_3,78
4,29_4,81
5,32_5,84
6,35_6,86562757598063