Cours de Statistiques (2e partie)

* Ce cours reprend dans ses grandes lignes le cours de Mme F. Duheille-Bienvenüe (MASS 42, 2001, Université Claude
Bernard - Lyon 1) dont on n'a pu qu'apprécier la clarté et la concision.
Chapitre 1. Méthodes de simulation d'un
échantillon.
Effectuer une simulation consiste à générer des données qui sont des réalisations de variables
déterministes ou aléatoires selon des lois données, afin d'étudier et de comprendre le fonctionnement
de systèmes économiques, industriels, scientifiques, politiques, etc.
Exemples : simulation d'un trafic urbain, de gestion d'un hôpital, d'évolution d'une population, de
variations boursières, etc.
Une simulation permet de provoquer le déroulement d'une expérience de façon rapide et
économique, et permet aussi d'éviter les dangers liés à la réalisation de certaines expériences à
l'échelle réelle. Elle permet aussi de répéter l'expérience en faisant varier les paramètres. Enfin elle
aide à l'élaboration de techniques de prévision et d'amélioration.
1.1. Méthodes de Monte-Carlo.
1.1.1. Principe d'une méthode de Monte-Carlo.
Une méthode de Monte-Carlo consiste à calculer un échantillon de loi
déterminée à partir d'un échantillon de loi uniforme (nombres choisis au hasard à
l'aide d'une table de nombres au hasard, ou nombres pseudo-aléatoires générés par
un logiciel).
Rappelons qu'on appelle n-échantillon indépendant tout n-uple (X 1, ... , X n) de
variables aléatoires indépendantes et identiquement distribuées (c'est-à-dire de
même loi), ou, si l'on aime les sigles ésotériques, VA iid.
Résultat fondamental : pour une variable aléatoire U de loi uniforme, ou
constante, sur l'intervalle [0, 1], X et F X–1 (U) ont la même loi de probabilité.
Condition : F X, fonction de répartition de X, est une bijection de R
RR
R sur ]0, 1[.
Etant donné un échantillon U 1, ... , U n, de nombres choisis au hasard dans
l'intervalle ] 0, 1 [, les variables aléatoires F X–1 (U 1), ... , F X–1 (U n), forment un
échantillon de la loi de X.
Cette méthode est utile pour :
— construire un échantillon de loi connue
p
ermettant d'étudier
Cours de Statistiques (2e partie) *
Henri IMMEDIATO
LICENCE Scientifi
q
ue

les paramètres d'un échantillon de loi inconnue,
— donner une estimation d'un paramètre, d'une constante,
d'une intégrale,
— etc.
1.1.2. Application pratique de la méthode de Monte-Carlo avec la fonction de
répartition.
Etant donnée une variable aléatoire X :
— on fixe a priori, à l'aide de la fonction de répartition de X,
pour chaque nombre choisi au hasard, une valeur de X (c'est ce
qu'on appelle la transformation par quantile).
— on tire au sort n nombres au hasard,
— on en déduit n valeurs de X qui constituent la réalisation
d'un échantillon de X.
1.1.2.1. Simulation d'une
variable aléatoire X de
Bernoulli de paramètre p.
— pour chaque nombre u i, 1
≤ i ≤ n, choisi au hasard dans
l'intervalle [0, 1] des valeurs
de la fonction de répartition,
on prend
x i = 0 si u i ∈ [0, 1 – p],
x i = 1 si u i ∈ ] 1 – p, 1].
Cela revient à tracer un trait
horizontal à l'ordonnée u i et à
regarder où il coupe la courbe représentative de la fonction de répartition de X, les points
de discontinuité étant rejoints par un trait vertical : l'abscisse du point d'intersection est
x i.
— (x 1, ... , x n) est la réalisation d'un n-échantillon de X :
P (X = 1) = P (U ∈ ] 1 – p, 1]) = p.
Remarque.
Dès qu'on sait simuler une loi de Bernoulli, on sait simuler les lois qui en dérivent : loi
géométrique (nombre d'épreuves pour arriver à un succès), somme de variables
géométriques de même paramètre (nombre d'épreuves pour arriver à k succès), loi
b
inomiale
(
nombre de succès en né
p
reuves
)
.

Exemple (engendré avec la fonction ALEA d'Excel).
Uniforme sur [0;1] 0.175 0.693 0.162 0.822 0.024 0.051 0.720 0.882 0.069 0.797 0.489 0.206 0.675 0.546 0.880 0.086 0.346 0.986 0.604 0.005
Bernoulli (0.32) 01010011010000100100
Geom*(0.32) 2 2 3 1 2 5 3
Somme de 2 Geom*(0.32) 4 4 7
Binom(20;0.32) 15
Uniforme sur [0;1] 0.133 0.230 0.802 0.210 0.351 0.806 0.850 0.238 0.282 0.166 0.371 0.332 0.521 0.115 0.751 0.428 0.999 0.065 0.516 0.533
Bernoulli (0.32) 00100110000000101000
Geom*(0.32) 5 3 1 8 2
Somme de 2 Geom*(0.32) 8 4 10
Binom(20;0.32) 22
Uniforme sur [0;1] 0.497 0.008 0.407 0.815 0.800 0.168 0.795 0.552 0.383 0.331 0.366 0.036 0.804 0.604 0.340 0.372 0.002 0.036 0.753 0.561
Bernoulli (0.32) 00011010000010000010
Geom*(0.32) 7 1 2 6 6
Somme de 2 Geom*(0.32) 8 8
Binom(20;0.32) 16
Uniforme sur [0;1] 0.507 0.315 0.122 0.554 0.387 0.506 0.199 0.025 0.831 0.292 0.862 0.105 0.240 0.651 0.352 0.487 0.027 0.650 0.116 0.281
Bernoulli (0.32) 00000000101000000000
Geom*(0.32) 10 2
Somme de 2 Geom*(0.32) 16
Binom(20;0.32) 16
Uniforme sur [0;1] 0.794 0.714 0.330 0.965 0.643 0.117 0.747 0.403 0.888 0.275 0.802 0.136 0.352 0.356 0.759 0.982 0.911 0.473 0.558 0.634
Bernoulli (0.32) 1 1 0 1 0 0 1 0 1 0 1 0 0 0 1 1 1 0 0 0
Geom*(0.32) 10 1 2 3 2 2 4 1 1
Somme de 2 Geom*(0.32) 12 3 5 6 2
Binom(20;0.32) 28

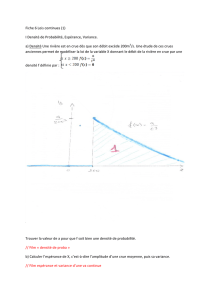
1.1.2.2. Simulation d'une variable aléatoire X de loi discrète à support borné ou
non.
— pour chaque nombre u i, 1 ≤ i ≤ n, choisi au hasard dans l'intervalle [0, 1] des valeurs
de la fonction de répartition, on prend pour valeur x i de X, l'abscisse du point
d'intersection de la droite d'ordonnée u i avec la courbe représentative de la fonction de
répartition de X.
— (x 1, ... , x n) est la réalisation d'un n-échantillon de X.
1.1.2.3. Simulation d'une
variable aléatoire X de loi
continue à support borné ou
non.
— pour chaque nombre u i, 1
≤ i ≤ n, choisi au hasard dans
l'intervalle [0, 1] des valeurs
de la fonction de répartition,
on prend pour valeur x i de X,
l'abscisse du point
d'intersection de la droite
d'ordonnée u i avec la courbe représentative de la fonction de répartition de X.
— (x 1, ... , x n) est la réalisation d'un n-échantillon de X.
— Si la fonction de répartition n'est continue que par morceaux, on joint les points de
discontinuité par des segments verticaux, la longueur du segment étant la probabilité de
l'abscisse.
1.1.3. Autres applications pratiques de la méthode de Monte-Carlo.
Comme il n'est pas toujours facile de déterminer la valeur de x i à partir de u i et de la fonction
de répartition de X, on utilise souvent des méthodes particulières à chaque type de loi.
1.1.3.1. Simulation d'une variable aléatoire X de loi géométrique sur N
NN
N* de
paramètre p.
— On a vu plus haut comment procéder. Au lieu d'utiliser la fonction de répartition, on
utilise la propriété de la loi géométrique sur N * : c'est la loi de probabilité du nombre
de répétitions d'une épreuve de Bernoulli qu'il faut pour atteindre un premier succès.
— On tire une suite de nombres au hasard dans l'intervalle [0, 1].
— On en déduit une suite de 0 ou 1, valeurs d'une variable de Bernoulli de paramètre p,
d'après 1.1.2.1 et la fonction de répartition de la variable de Bernoulli.
— Dans cette suite, on compte le nombre de termes x 1 qu'il faut pour atteindre un 1
(premier succès de l'épreuve de Bernoulli), puis le nombre x 2 de termes suivants, qu'il
faut
p
our atteindre le 1 suivant, etc.

— La suite des x i est un échantillon de loi géométrique sur N * de paramètre p.
— L'inconvénient de la méthode est qu'il faut en moyenne nombres aléatoires u i pour
engendrer une valeur x i.
L'avantage de la méthode est qu'elle dispense du calcul de logarithme nécessité par la
fonction réciproque de la fonction de répartition de la loi géométrique :
X = 1 + , où [ x ] désigne la partie entière de x.
1.1.3.2. Simulation d'une variable aléatoire X de loi binomiale de paramètres n et
p.
— On a vu plus haut comme procéder. Au lieu d'utiliser la fonction de répartition, on
utilise la propriété de la loi binomiale de paramètres n et p : c'est la loi de probabilité du
nombre de succès dans la répétition n fois d'une épreuve de Bernoulli.
— On tire une suite de nombres au hasard dans l'intervalle [0, 1].
— On en déduit une suite de 0 ou 1, valeurs d'une variable de Bernoulli de paramètre p,
d'après 1.1.2.1 et la fonction de répartition de la variable de Bernoulli.
— Dans cette suite, on compte le nombre de succès x 1 qu'on obtient en n épreuves,
puis le nombre x 2 de succès dans les n épreuves suivantes, etc.
— La suite des x i est un échantillon de loi binomiale de paramètres n et p.
— L'inconvénient de la méthode est qu'il faut n nombres aléatoires u i pour engendrer
une valeur x i.
L'avantage de la méthode est qu'elle dispense du calcul de la fonction réciproque de
la fonction de répartition de la loi binomiale.
Méthode alternative.
— On tire une suite (u i) 1 ≤ i ≤ n
de nombres au hasard dans
l'intervalle [0, 1].
— Pour chaque indice i, on
pose y 1 = u i, puis
y j + 1 =
,
pour 1 ≤ j ≤ k – 1.
On désigne par x i le
nombre de y j compris entre 1 – p et 1.
Explication.
Cet algorithme revient à définir, à partir de la variable aléatoire U de loi uniforme sur [0,
1], d'abord une suite (Y j) 1 ≤ j ≤ k de variables aléatoires à valeurs dans [0, 1] par Y 1 = U
p
uis