Annales de mathématiques bac S 2014
Annales
de mathématiques
du baccalauréat scientifique
Édition 2014
Sujets & corrigés détaillés
Éric Guirbal
Professeur indépendant, Toulouse
Éric GUIRBAL
Professeur indépendant de mathématiques
Toulouse
B
CE DOCUMENT EST EN CH A N T I E R.
Les mises à jour se font en continu et sont disponibles à l’adresse
Version du 18 juin 2014.
Ce document est distribué selon les termes de la licence Creative Commons
Attribution - Pas d’utilisation commerciale - Partage à l’identique 3.0 France.
Sommaire
1 Pondichéry 1
Énoncé .................................... 1
Corrigé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2 Liban 25
Énoncé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
Corrigé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34
3 Amérique du Nord 47
Énoncé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
Corrigé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
4 Centres étrangers 71
Énoncé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
Corrigé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
5 Métropole 95
Énoncé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
Corrigé . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96
iii
ÉNONCÉ
Sujet 1
Pondichéry
8 avril 2014
ÉNONCÉ
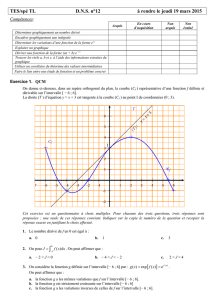
Exercice 1 (4 points)
Commun à tous les candidats.
Dans cet exercice, sauf indication contraire, les résultats seront arrondis
au centième.
1.
La durée de vie, exprimée en années, d’un moteur pour automatiser un
portail fabriqué par une entreprise A est une variable aléatoire
X
qui suit
une loi exponentielle de paramètre
λ
, où
λ
est un réel strictement positif.
On sait que P(X É2) =0,15.
Déterminer la valeur exacte du réel λ.
Dans la suite de l’exercice on prendra 0,081 pour valeur de λ.
2. a. Déterminer P(X Ê3).
b. Montrer que pour tous réels positifs tet h,
PXÊt(X Êt+h)=P(X Êh).
c.
Le moteur a déjà fonctionné durant 3 ans. Quelle est la probabilité
pour qu’il fonctionne encore 2 ans?
d.
Calculer l’espérance de la variable aléatoire
X
et donner une interpré-
tation de ce résultat.
3.
Dans la suite de cet exercice, on donnera des valeurs arrondies des résultats
à10−3.
L’entreprise A annonce que le pourcentage de moteurs défectueux dans
la production est égal à 1 %. Afin de vérifier cette affirmation 800 mo-
teurs sont prélevés au hasard. On constate que 15 moteurs sont détectés
défectueux.
1
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
1
/
100
100%
