Polygones réguliers

Problème
On rappelle que l'aire d'un triangle se calcule par la formule :
base×hauteur
2
Rémy dispose de 96 m de grillage avec lesquels il souhaite construire un enclos pour son poney. Il cherche quelle
forme donner à son enclos pour que celui-ci ait la plus grande surface possible.
Toutes les parties sont indépendantes
Partie 1
Sa première idée est de réaliser un rectangle avec les 96 m de grillage.
Calculer la longueur et la largeur de ce rectangle sachant que :
– la longueur est le double de la largeur.
– son périmètre est 96 m.
Calculer l’aire de ce rectangle de 96 m de périmètre.
Partie 2
Sa deuxième idée est de réaliser un carré. Calculer l’aire d’un carré de 96 m de périmètre.
Partie 3
Sa troisième idée est de réaliser un hexagone régulier.
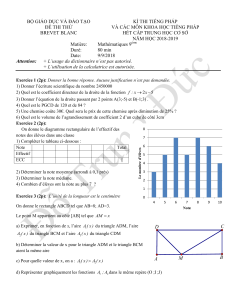
Le schéma à main levée ci-contre représente un
hexagone régulier ABCDEF de 96 m de périmètre.
Il est inscrit dans un cercle de centre O et de rayon 16 m.
Le segment [OH] est une hauteur du triangle équilatéral OBA.
1. Calculer la longueur OH, exprimée en m.
En donner l’arrondi au centimètre près.
2. Utiliser ce résultat pour calculer l’aire du triangle OBA, exprimée en m²
et arrondi au 1/10.
3. En déduire l’arrondi à l’unité de l’aire d’un hexagone régulier de 96 m
de périmètre.
Partie 4
Sa quatrième idée est de réaliser un octogone régulier de 96 m
de périmètre.
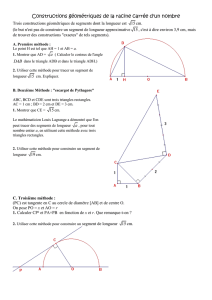
La figure à droite représente le plan réalisé par Rémy.
Cet octogone est inscrit dans un cercle de centre I. Le segment [IK]
est une hauteur du triangle isocèle IMN.
1. Vérifier que MN = 12 m dans la réalité.
2. Combien mesure l'angle
̂
NIM
puis l'angle
̂
MNI
?
3a. En prenant pour échelle 1 cm pour 3 m, représenter le triangle IMN,
puis le point K. Laisser apparents tous les traits de construction.
3b. Mesurer sur votre plan la longueur IK.
Combien de mètres cela représente-t-il dans la réalité ?
Si tu n'as pas ton matériel trouve la longueur IK par un autre moyen.
4. En déduire l’aire du triangle MIN, puis, à partir de cette valeur, calculer
l’aire d’un octogone régulier de 96 m de périmètre.
Partie 5
Les recherches ont permis à Rémy de remarquer que l’aire d’un polygone régulier de 96m de périmètre semble
augmenter quand on augmente le nombre de ses côtés. Il imagine qu’un enclos circulaire aurait peut-être une surface
encore plus grande.
1. Quel rayon faut-il prendre pour avoir un disque de périmètre 96 m?
2. En déduire l’aire d’un disque ayant pour périmètre 96 m.

Correction
Partie 1
Soit
x
la largeur du rectangle. Comme la longueur est le double de la largeur, la longueur du rectangle est
2x
.
Le périmètre du rectangle est alors
x+2x+x+2x
soit
6x
.
Résolvons l'équation
6x=96
. Nous avons
x=96
6=16
.
La largeur est de 16 m et la longueur de
16×2=32
m.
16×32=512
L'aire du rectangle est 512m².
Partie 2
Soit
x
la longueur d'un côté du carré, nous avons
4x=96
et donc
x=96
4=24
.
24×24=576
L'aire du carré est 576 m².
Partie 3
Le triangle OBA est équilatéral donc OB=OA=AB=16.
1. Le triangle OHB est rectangle en H, donc, d'après le théorème de Pythagore, nous avons :
OB²=OH²+HB² ; 16²=OH²+8² ; 256=OH²+64 ; OH²=256-64 ; OH²=192 or OH est une longueur donc OH>0 donc
OH =
√
192
soit environ 13,86 m.
2.
13,86×16
2=110,9
.
L'aire du triangle OAB est 110,9m².
3. Un hexagone est constitué de 6 triangles d'aire 110,9 m².
110,9×6=665,4
L'aire de l'hexagone est 665,4 m².
Partie 4
1.
96
8=12
Un côté de l'octogone mesure bien 12 m.
2.
̂
MIN
= 360°/8=45°. L'angle
̂
MIN
mesure 45°.
Comme le triangle IMN est isocèle (IN=IM), nous savons que
̂
NMI =
̂
INM
et comme la somme des angles d'un
triangle vaut 180°,nous avons
̂
MIN
+
̂
NMI +
̂
INM
=180° et donc
45°+2×
̂
NMI =180°
soit
2×
̂
NMI =180 °−45°=135 °
.
Nous avons ainsi
̂
NMI =
̂
INM =135 °
2=67,5°
.
3a. Nous devons tracer le triangle IMN. La difficulté est que nous ne
connaissons pas IM ou IN. Nous savons que :
- MN = 12 m soit 4 cm sur notre dessin
-
̂
MIN
= 360°/8=45°
- IN=IM car le triangle est isocèle.
Pour tracer le triangle IMN, il faut d'abord tracer le segment MN de 4 cm
puis tracer deux marques avec le rapporteur pour que les angles
̂
NMI et
̂
INM
valent 67,5°.
3b. Sur le plan IK mesure 4,8 cm soit 14,4 m dans la réalité.
Si vous n'avez pas votre matériel faites un peu de trigonométrie dans le
triangle IKM rectangle en K.
4.
14,4×12
2=86,4
L'aire du triangle MIN est 86,4m² environ.
L'octogone est composé de 8 triangles de cette aire-là.
86,4×8=691,2
L'octogone a pour aire 691,2 m².
Partie 5
1. Soit
R
le rayon du disque, nous avons
2×π×R=96
et donc
R=96
2×π
ce qui donne un rayon mesurant environ
15,28 m.
2. L'aire du disque est donné par la formule :
π×R2
, ici comme
R≈15,28
nous avons une aire environ égale à 733
m². C'est l'aire la plus grande possible.