Variables continues usuelles

Variables continues usuelles
I) Variables uniformes
1.1 Densités
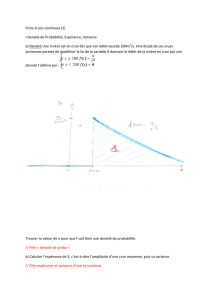
Nous avons déjà rencontré ce type de variables.
Définition 1
On dit que la variable  suit une loi uniforme continue sur  si sa fonction densité de
probabilité est donnée par :   
   .
On écrit que 
Définition 2
On dit que la variable  suit une loi uniforme continue sur  si sa fonction densité de
probabilité est donnée par :   
   .
On écrit que 
1.2) Fonctions de répartition
On a vu que
Théorème
Si  sa fonction de répartition est 
   .
Si  sa fonction de répartition est 
   .
1.3) Espérances et variances
Soit 
On a  
On a 
Donc 

Si   on fait  et  dans les formules ci-dessus.
On trouve : 
II) La loi exponentielle
2.1) Densité de probabilité
Théorème et définition
Soit λ un réel strictement positif. La fonction  définie sur  par    
est une densité de probabilité.
Si  est une variable aléatoire dont  est une densité, on dit que  suit une loi exponentielle
de paramètre λ.
La fonction  est bien évidemment positive, continue sauf en 0.
On a  
On a également 
On a donc 
Donc  
Et donc  
La fonction  est bien une densité de probabilité.
2 .2) Fonction de répartition
Soit une variable  qui suit une loi exponentielle de paramètre λ. On pourra écrire 
Sa fonction de répartition  est définie sur  par :
Nous avons vu que  
On a 

Si  on aura  
On a donc    
2.3) Espérance et variance
On a sous réserve de convergence  
On a pour  
On procède par intégration par parties :
On a  de classe   et  est continue.
On pose : 
On a donc  
On a 
Donc  
Et donc  
Calculons 
Sous réserve de convergence, on a :
On déterminer l’intégrale 

On procède encore à une intégration par parties.
La fonction  est de classe  sur  et la fonction  est continue sur .
On pose 
On a donc 
Donc  
On a par croissance comparée
On a donc 
Donc 
Théorème
Soit  une variable aléatoire qui suit une loi exponentielle de paramètre λ. Alors  admet une
espérance et une variance données par les formules :
2.4) Discrétisation d’une loi exponentielle
On considère une variable continue  qui suit une loi exponentielle de paramètre λ.
Soit  une variable à valeur dans  définie par
Quelle est la loi de la variable 
On a puisque  
Posons 
 On a  donc 
On a

On a donc 
La variable  suit donc une loi géométrique de paramètre 
III) La loi normale
3.1) Des fonctions de densité particulières
Considérons la fonction définie sur  par 
Cette fonction est évidemment définie, continue et positive sur .
On démontre et nous admettrons qu’elle remplit également la propriété :
Cette fonction est une densité de probabilité.
Soit  un nombre réel quelconque et σ un nombre réel strictement positif.
Soit  la fonction définie sur  par 
Cette fonction est évidemment définie, continue et positive sur .
En effet par croissance comparée, on a facilement
Ce qui implique qu’il existe  , tel que
Ce qui permet de conclure en +∞.
De même, on a 
On aura donc les mêmes conclusions en considérant la fonction de Riemann sur un intervalle
 où 
Posons 
Quand , on a aussi  Quand  on a également 
On a 
On peut donc écrire :