calculs de primitives et d`intégrales

Christophe Bertault — Mathématiques en MPSI
CALCULS DE PRIMITIVES ET D’INTÉGRALES
Ce chapitre vise à renforcer votre pratique du calcul intégral au moyen de révisions ciblées et grâce à deux nouveautés,
l’intégration par parties et le changement de variable. Le point de vue adopté n’est pas théorique. Nous définirons proprement
la notion d’intégrale et nous démontrerons le théorème fondamental du calcul intégral sur lequel ce chapitre repose au
chapitre « Intégration sur un segment » en fin d’année.
Dans tout ce chapitre, Kest l’un des ensembles Rou Cet Iet Jsont des intervalles.
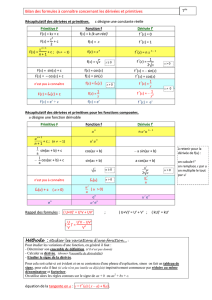
1CALCULS SIMPLES DE PRIMITIVES
Définition (Primitive) Soit f:I−→ Kune fonction. On dit qu’une fonction F:I−→ Kest UNE primitive de f sur I si
Fest dérivable sur Ide dérivée f.
Exemple La fonction x7−→ x2
2est UNE primitive de x7−→ xsur Ret Arctan est UNE primitive de x7−→ 1 1+x2sur R.
Théorème (« Unicité » des primitives à constante additive près) Soit f:I−→ Kune fonction. On suppose que f
possède une primitive F:I−→ K. Les primitives de fsur Ià valeurs dans Ksont alors toutes les fonctions F+λ,λ
décrivant K.
$ATTENTION !$Il n’existe jamais une seule primitive, on ne dit jamais « la » primitive mais UNE primitive. Il peut ne
pas en exister, mais s’il en existe, il en existe une infinité et elles sont toutes égales à constante additive près.
Démonstration Pour tout e F∈ D(I,K):e Fest une primitive de f⇐⇒ e F′=f⇐⇒ e F′=F′
⇐⇒ e F−F′=0⇐⇒ e
F−Fest constante ⇐⇒ ∃ λ∈K/e F=F+λ.
$ATTENTION !$Les fonctions que l’on manipule couramment sont un empilement de fonctions usuelles liées entre
elles par des additions, des multiplications, des passages à l’inverse et des compositions. Vous savez toutes les dériver car
vous savez dériver les fonctions usuelles et disposez des formules de dérivation d’une somme, d’un produit, d’un inverse et
d’une composée.
La primitivation des fonctions est autrement plus difficile :
— vous savez primitiver la fonction x7−→ x, mais pour primitiver son inverse x7−→ 1
x, il a fallu qu’on vous introduise
une nouvelle fonction usuelle, la fonction logarithme,
— vous savez primitiver la fonction x7−→ 1+x2, mais pour primitiver son inverse x7−→ 1
1+x2, il a fallu qu’on vous
introduise une nouvelle fonction usuelle, la fonction arctangente.
On ne peut pas dire pourtant que les fonctions x7−→ 1
xet x7−→ 1 1+x2soient compliquées ! Le problème de la primitivation,
c’est qu’on ne peut pas primitiver explicitement toutes les fonctions qu’on utilise couramment. On peut montrer — mais
c’est difficile — que les primitives d’une fonction simple comme x7−→ e−x2ne peuvent en aucune manière être écrites
explicitement comme un empilement de fonctions usuelles — à moins bien sûr de considérer une telle primitive comme
nouvelle fonction usuelle ! On retiendra notamment de ces remarques la mise en garde suivante :
En général, même quand on sait primitiver deux fonctions,
on NE sait PAS primitiver leur PRODUIT, leur QUOTIENT, leur COMPOSÉE.
1

Christophe Bertault — Mathématiques en MPSI
En pratique La mise en garde précédente ne signifie heureusement pas qu’on ne sait rien faire. En particulier,
toute fonction de la forme f′×g′◦fadmet g◦fpour primitive et on attend de vous que vous sachiez repérer une telle
forme. Mentionnons rapidement quelques cas très courants :
u′euse primitive en eu,u′
uen ln |u|,u′uα(α6=−1) en uα+1 α+1,u′cos uen sin u,u′ 1+u2en Arctan u, etc.
Si Fest une primitive de f, alors pour tout a∈C∗et b∈C,x7−→ F(ax +b)
aest une primitive de x7−→ f(ax +b).
Exemple La fonction x7−→ sin x
5−3 cos xadmet x7−→ 1 3ln 5−3 cos xpour primitive sur R, la fonction x7−→ epx
pxadmet
x7−→ 2 epxpour primitive sur R∗
+et la fonction x7−→ 1
4x2+1admet x7−→ 1 2Arctan(2x)pour primitive sur R.
En pratique Le programme exige que vous sachiez primitiver les fonctions de la forme x7−→ 1
ax2+bx +cavec
a,b,c∈R,a6=0 et b2−4ac <0 — discriminant négatif, le dénominateur ne s’annule pas sur R. C’est très simple, on écrit
«ax2+bx +c» sous FORME CANONIQUE, on fait apparaître la dérivée d’arctangente et enfin on primitive. Il est ici assez
utile de savoir que :
Pour tout a>0, x7−→ 1
aArctan x aest une primitive de x7−→ 1 x2+a2.
Exemple La fonction x7−→ 1
3x2−x+1admet x7−→ 2
p11 Arctan 6x−1 p11 pour primitive sur R.
En effet Pour tout x∈R:1
3x2−x+1=1 3×1
x2−x
3+1 3
=1
3×1
x−1
62
+11
36
=1
3×1
x−1
62
+p11
62,
donc x7−→ 1
3x2−x+1admet pour primitive x7−→ 1 3×6
p11 Arctan 6 p11 x−1
6=2
p11 Arctan 6x−1 p11 .
En pratique On a souvent besoin de primitiver les fonctions de la forme x7−→ eax cos(bx)et x7−→ eax sin(bx)
avec a,b∈R∗. C’est très simple. Pour tout x∈R: eax cos(bx) = Ree(a+ib)x. Or x7−→ e(a+ib)xadmet x7−→ e(a+ib)x
a+ib
pour primitive, donc x7−→ eax cos(bx)admet pour primitive :
x7−→ Re e(a+ib)x
a+ib=eax a2+b2Recos(bx) + i sin(bx)×(a−ib)=eax a2+b2acos(bx) + bsin(bx).
En pratique Autre technique bien utile, la LINÉARISATION. Grâce à elle, nous savons calculer toutes les primitives
de fonctions telles que x7−→ sin2xcos3(4x)— produits de sinus et de cosinus.
En pratique Pour finir, on primitive les fractions rationnelles en primitivant leur DÉCOMPOSITION EN ÉLÉMENTS
SIMPLES. Nous nous contenterons de calculs simples à ce stade, conformes à l’esprit du petit chapitre « Introduction à la
décomposition en éléments simples ».
Exemple La fonction x7−→ 1
xx2+1admet x7−→ ln |x|
px2+1pour primitive sur R∗.
En effet
•Forme de la décomposition en éléments simples : La fraction 1
XX2+1a une partie entière nulle,
donc pour certains a,b,c∈R:Æ1
XX2+1=a
X+bX +c X2+1.
•Calcul de a:On multiplie Æpar Xpuis on évalue en 0 : a=1.
•Calcul de b:On multiplie Æpar X, puis on évalue en un réel xqu’on fait tendre vers +∞: 0 =a+b,
donc b=−1.
•Calcul de c:On évalue Æen 1 : 1
2=a+b+c 2, donc c=0.
2

Christophe Bertault — Mathématiques en MPSI
•Primitivation : Nous venons d’établir que : 1
XX2+1=1
X−X X2+1. La fonction x7−→ 1
xx2+1
admet ainsi comme voulu x7−→ ln |x|− 1
2ln x2+1=ln |x|
px2+1pour primitive sur R∗.
2LIEN ENTRE LES NOTIONS DE PRIMITIVE ET D’INTÉGRALE
Définition (Fonction complexe continue) Soit f:I−→ Cune fonction. On dit que fest continue sur I si Re(f)et
Im(f)le sont.
L’ensemble des fonctions complexes continues sur Iest noté C(I,C).
L’intégrale d’une fonction continue vous a été définie en Terminale comme une aire ALGÉBRIQUE sous la courbe — ce
qui veut dire que les portions de la courbe situées SOUS l’axe des abscisses contribuent négativement au calcul de l’aire.
Cette définition est totalement bancale car nous sommes au fond bien incapables de définir la notion d’aire, mais nous nous
contenterons de cette approche pour le moment. L’intégrale sera définie proprement plus tard au chapitre « Intégration sur
un segment ».
Définition (Intégrale sur un segment d’une fonction complexe continue) Soient f∈ C(I,C)et a,b∈I. On appelle
intégrale de f de a à b le nombre complexe Zb
a
f(t)dt=Zb
a
Re(f)(t)dt+iZb
a
Im(f)(t)dt.
$ATTENTION !$Une intégrale de fonction complexe ne peut pas être interprétée comme une aire algébrique, c’est
un nombre complexe !
Théorème (Propriétés de l’intégrale d’une fonction continue) Soient f,g∈ C(I,C)et a,b,c∈I.
•Linéarité : Pour tous λ,µ∈C:Zb
aλf(t) + µg(t)dt=λZb
a
f(t)dt+µZb
a
g(t)dt.
•Relation de Chasles : Zc
a
f(t)dt=Zb
a
f(t)dt+Zc
b
f(t)dt.
•Inégalité triangulaire : Si a¶b:Zb
a
f(t)dt¶Zb
af(t)dt.
Les trois propriétés qui suivent, parce qu’elles cachent l’utilisation d’inégalités, n’ont de sens que pour des fonctions
RÉELLES.
Théorème (Propriétés de l’intégrale d’une fonction réelle continue) Soient f,g∈ C(I,R)et a,b∈I.
•Positivité : Si f¾0 et si a¶b, alors Zb
a
f(t)dt¾0.
•Positivité stricte : Si fest strictement positive sauf éventuellement en un nombre fini de points et si a<b, alors
Zb
a
f(t)dt>0.
•Croissance : Si f¶get a¶b, alors Zb
a
f(t)dt¶Zb
a
g(t)dt.
3

Christophe Bertault — Mathématiques en MPSI
Théorème (Théorème fondamental du calcul intégral) Soient f∈ C(I,C)et a,b∈I.
(i) La fonction x7−→ Zx
a
f(t)dtest une primitive de fsur I.
Pour tout A∈C, il existe une et une seule primitive de fsur Ide valeur Aen a, la fonction x7−→ A+Zx
a
f(t)dt.
(ii) Pour toute primitive Fde f:Zb
a
f(t)dt=F(b)−F(a). On note [F]b
aou F(x)x=b
x=acette quantité F(b)−F(a).
Démonstration L’assertion (ii) découle de l’assertion (i). La fonction Fest une primitive de fqui vaut F(a)
en aet c’est la seule, donc d’après (i), F(x) = F(a) + Zx
a
fpour tout x∈I. Il reste à évaluer en b.
Explication 
•L’assertion (i) est un théorème d’EXISTENCE de primitives pour les fonctions CONTINUES.
•Fondamental, ce théorème l’est parce qu’il établit un lien entre des notions apparemment totalement étrangères — la
notion d’aire/intégrale et la notion de primitive, liée à la dérivation. Quelle intuition cela exprime-t-il ?
Supposons fréelle et notons Fla fonction x7−→ Zx
a
f(t)dt. Ci-contre, l’aire
algébrique colorée à gauche vaut : Zx+h
x
f(t)dt=F(x+h)−F(x). Or si
hest tout petit, sachant que fest CONTINUE en x, on peut considérer que fest
approximativement égale à f(x)sur tout le segment [x,x+h], et donc on peut
approximer l’aire colorée à gauche par l’aire colorée à droite, qui vaut h f (x)
selon le principe « base ×hauteur ».
y=f(x)
xx+h
h
≈
h
f(x)
Conclusion : F(x+h)−F(x)≈h f (x)pour htout petit, ou encore : lim
h→0
F(x+h)−F(x)
h=f(x). Par définition
du nombre dérivé, on comprend mieux ainsi pourquoi Fest dérivable de dérivée f.
Exemple Z2π
0
sin tdt=−cos 2π
0=0 et Z2π
0|sin t|dt=Zπ
0
sin tdt−Z2π
π
sin tdt=−cos π
0−−cos 2π
π=4.
Exemple Pour tout α∈R+:Z1
0
xαdx=xα+1
α+1x=1
x=0
=1
α+1. Intégrale très courante, à connaître PAR CŒUR !
$ATTENTION !$On rencontre parfois dans les livres de mystérieuses intégrales sans bornes — par exemple :
Zt2+2tdt=t3
3+t2,Zdx x=ln x,Zsin θdθ=−cos θou Z2ucos u2du=sin u2.
Cette notation sans bornes est utilisée pour son efficacité calculatoire comme nous allons le voir, mais elle n’a AUCUN SENS
À PROPREMENT PARLER puisqu’on primitive toujours à constante additive près. Je répète et j’insiste, cette notation est bien
commode mais NE DÉSIGNE AUCUN OBJET MATHÉMATIQUE.
Exemple La fonction x7−→ e−xsin xadmet x7−→ −e−x
2sin x+cos xpour primitive sur R.
En effet Ze−xsin xdx=ZIme(−1+i)xdx=Im Z e(−1+i)xdx=Im e(−1+i)x
−1+i=−e−x 2Im(1+i)eix
=−e−x
2sin x+cos x.
4

Christophe Bertault — Mathématiques en MPSI
Exemple La fonction xϕ
7−→ Zx2
x
e−t2dtest dérivable sur Rde dérivée x7−→ 2xe−x4−e−x2.
En effet La fonction t7−→ e−t2est continue sur Rdonc xF 7−→ Zx
0
e−t2dten est une primitive. Or pour tout
x∈R:ϕ(x) = Fx2−F(x), donc ϕest dérivable de dérivée x7−→ 2x F ′x2−F′(x) = 2xe−x4−e−x2.
3INTÉGRATION PAR PARTIES
Définition (Fonction de classe C1)Soit f:I−→ Kune fonction. On dit que fest de classe C1sur I si fest dérivable
sur Iet si f′est continue sur I.
L’ensemble des fonctions de classe C1sur Ià valeurs dans Kest noté C1(I,K).
$ATTENTION !$Ne confondez pas « dérivable à dérivée continue », i.e. « de classe C1», et « dérivable ET continue ».
Comme la dérivabilité implique la continuité, « dérivable ET continue » est une maladresse que vous me ferez le plaisir
d’éviter !
Exemple Toute primitive d’une fonction continue est de classe C1puisque sa dérivée, justement, est continue.
Théorème (Intégration par parties) Soient u,v∈ C1(I,C)et a,b∈I.
Zb
a
u′(t)v(t)dt=uvb
a−Zb
a
u(t)v′(t)dt.
Démonstration Comme uet vsont de classe C1, les fonctions (uv)′,u′vet uv′sont continues, donc d’après
le théorème fondamental du calcul intégral et par linéarité de l’intégrale :
uvb
a=Zb
a
(uv)′(t)dt=Zb
au′(t)v(t) + u(t)v′(t)dt=Zb
a
u′(t)v(t)dt+Zb
a
u(t)v′(t)dt.
Exemple Zπ
0
tcos tdt=Zπ
0
u′(t)
z}|{
cos t×
v(t)
z}|{
tdtIPP =tsin tt=π
t=0−Zπ
0
sin tdt=−Zπ
0
sin tdt=−−cos tt=π
t=0=−2.
Exemple Z1
0
t3et2dt=1
2Z1
0
u′(t)
z}|{
2tet2×
v(t)
z}|{
t2dtIPP =1
2t2et2t=1
t=0−1
2Z1
0
2tet2dt=e
2−1 2et2t=1
t=0=1
2.
En pratique On peut aussi pratiquer des intégrations par parties sur des intégrales sans bornes pour calculer des
primitives. La formule prend ici la forme suivante : Zu′(t)v(t)dt=u(t)v(t)−Zu(t)v′(t)dt.
Exemple La fonction logarithme admet x7−→ xln x−xpour primitive sur R∗
+.
En effet Zln xdx=Zu′(x)
z}|{
1×
v(x)
z}|{
ln xdxIPP =xln x−Zx×1
xdx=xln x−Zdx=xln x−x.
5