correction - maths

1S DS no5Dur´ee :1h
Exercice 1 ( 4 points )
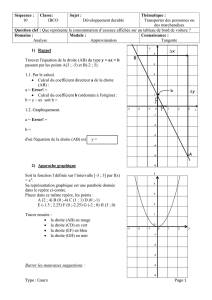
Voici la courbe repr´esentative Cfd’une fonction fd´efinie sur [−6; 9] avec quatre de ses tangentes.
Le point Ade coordonn´ees (−2,4; 0), appartient `a la courbe Cf
1. D’apr`es le graphique, donner la valeur de f(−2) puis la valeur de f0(−5), f0(2) et f0(6,5)
Justifier soigneusement la r´eponse pour f0(2).
*Solution:
Le point de coordonn´ees (−2; 1) appartient `a la courbe donc f(−2) = 1
f(−2) = 1
f0(−5) est le coefficient directeur de la tangente `a la courbe au point d’abscisse −5
et cette tangente est parall`ele `a l’axe des abscisses donc a pour coefficient directeur 0
f0(−5) = 0
Remarque
On peut aussi lire directement le coefficient directeur en calculant `a partir du graphique f0(−2) =
variation des ordonn´ees
variation des abscisses =+2 +1 = 2 (voir graphique en rouge)
De mˆeme, f0(2) est le coefficient directeur de la tangente `a la courbe au point d’abscisse 2
et cette tangente passe par les points D(2; 0,5) et E(5; −1,5)
donc f0(2) = −2
3(trac´e en bleu sur le graphique)
f0(−2) = −2
3
De mˆeme, f0(6,5) est le coefficient directeur de la tangente `a la courbe au point d’abscisse 6,5
donc f0(6,5) = +2,5
+2 =5 4= 1,25 (trac´e en vert sur le graphique)
f0(−2) = 5
4

2. D´eterminer l’´equation de la tangente `a Cfau point d’abscisse 6,5.
*Solution:
La tangente au point d’abscisse 6,5 a pour coefficient directeur f0(6,5) = 5
4
et admet donc une ´equation r´eduite de la forme y=5
4x+b(b∈R)
et passe par le point de la courbe de coordonn´ees (6,5; 2), si on note Fce point, on a donc :
yF=5
4xF+b⇐⇒ 2 = 5 4×6,5 + b⇐⇒ b= 2 −32,5 4⇐⇒ b=−24,5 4
La tangente `a la courbe au point d’abscisse 6,5 a pour ´equation r´eduite y=5
4x−24,5 4
Remarque
Avec la ”formule” donnant directement l’´equation r´eduite de la tangente, on a :
y=f0(a)(x−a) + f(a) avec a= 6,5, f0(a) = 5
4et f(a) = 2
3. On sait que f0(−3) = 2 ; tracer T−3, tangente `a la courbe Cfau point d’abscisse −3.
*Solution:
f0(−3) est le coefficient directeur de la tangente T−3au point de la courbe d’abscisse −3
Trac´e en orange sur le graphique.
Exercice 2 ( 3 points )
Soit la fonction gd´efinie sur Rpar g(x) = 2x2−x+ 1.
A l’aide du taux d’accroissement, montrer que gest d´erivable en a= 1 et calculer g0(1).
*Solution:
Pour tout r´eel h6= 0, le taux d’accroissement de fentre a= 1 et b= 1 + hest :
T(h) = f(1 + h)−f(1)
1 + h−1=f(1 + h)−f(1) h
•Calcul de f(1) et f(1 + h)
f(1 + h) = 2(1 + h)2−(1 + h) + 1 = 2(1 + 2h+h2)−1−h+ 1 = 2 + 4h+ 2h2−h= 2h2+ 3h+ 2
et f(1) = 2 −1 + 1 = 2
•Calcul de T(h) :
T(h) = f(1 + h)−f(1)
h=2h2+ 3h+ 2 −2 h=h(2h+ 3) h= 2h+ 3
•Limite quand h−→ 0
Quand h−→ 0, on a T(h)−→ 3
avec les notations des limites : lim
h→0T(h) = 3
•Conclusion
La limite de T(h) quand h−→ 0 existe et est finie
donc fest d´erivable en x= 1 et f0(1) = 3
RemarqueEn utilisant la fonction d´eriv´ee de favec les formules de d´erivation, on a :
f0(x) = 2 ×2x−1 + 0 = 4x−1
et donc f0(1) = 4 −1 = 3

Exercice 3 ( 3 points )
La fonction fest d´efinie sur Rpar f(x) = x3.
D´emontrer que f0(x) = 3x2pour tout r´eel x.
aide : (a+b)3=a3+ 3a2b+ 3ab2+b3
*Solution:
Pour tout r´eel a∈Ret tout r´eel h6= 0, le taux d’accroissement de fentre aet b=a+hest :
T(h) = f(a+h)−f(a)
a+h−a=f(a+h)−f(a) h
•Calcul de f(a) et f(a+h) en fonction de a
f(a+h) = (a+h)3=a3+ 3a2h+ 3ah2+h3
et f(a) = a3
•Calcul de T(h) :
T(h) = f(a+h)−f(a)
h=a3+ 3a2h+ 3ah2+h3−a3 h=h(3a2+ 3ah +h2) h= 3a2+ 3ah +h2
•Limite quand h−→ 0
Quand h−→ 0, on a T(h)−→ 3a2
avec les notations des limites : lim
h→0T(h) = 3a2
•Conclusion
Pour tout r´eel a, la limite de T(h) quand h−→ 0 existe et est finie
donc fest d´erivable sur Ret f0(x) = 3x2
Exercice 4 ( 10 points )
1. La fonction fest d´efinie et d´erivable sur R∗par f(x) = 3x2
2+ 3x−1 + 1 x2.
Calculer f0(x)(simplifier l’expression obtenue)
*Solution:
f(x) = 3
2x2+ 3x−1 + 1 x2
Rappel : (x2)0= 2x, (3x−1)0= 3 et ( 1
x2)0=−2 x3
donc f0(x) = 3
2×2x+3+−2 x3
f0(x) = 3x+ 3 −2
x3
2. La fonction gest d´efinie par g(x) = (2x+ 1)√x
a) D´eterminer l’ensemble de d´efinition Dgde g.
*Solution:
La fonction racine carr´ee est d´efinie sur [0; +∞[
Dg= [0; +∞[

b) Justifier que gest d´erivable sur ]0; +∞[, et calculer g0(x)(simplifier l’expression obtenue).
*Solution:
u:x7−→ √xest d´erivable sur ]0; +∞[
et v:x7−→ 2x+ 1 (fonction affine) est d´erivable sur Rdonc sur ]0; +∞[
donc le produit de uet vest d´erivable sur ]0; +∞[.
gest donc d´erivable sur ]0; +∞[
On pose donc u(x) = 2x+ 1 et v(x) = √x
On a donc u0(x) = 2 et v0(x) = 1
2√x
g0(x) = u0(x)v(x) + u(x)v0(x)
= 2√x+ (2x+ 1) ×1
2√x
= 2√x+2x+ 1
2√x
=2√x×2√x+ 2x+ 1
2√x
=6x+ 1
2√x
g0(x) = 6x+ 1
2√x
3. La fonction hest d´efinie sur Dh=R\3
5par h(x) = 4x−1 3−5x.
a) Justifier que hest d´erivable sur Dh.
*Solution:
u:x7−→ 4x−1 est d´erivable sur Rdonc sur Dh
et v:x7−→ 3−5xest d´erivable sur Rdonc sur Dhet pour tout x∈Dh,v(x)6= 0
donc le quotient de upar vest d´erivable sur Dh
donc hest d´erivable sur Dh
b) Calculer h0(x).
*Solution:
On pose u(x) = 4x−1 et v(x) = 3 −5x
et on a u0(x) = 4 et v0(x) = −5
h0(x) = u0(x)v(x)−u(x)v0(x)
(v(x))2=(4)(3 −5x)−(4x−1)(−5) (3 −5x)2=12 −20x+ 20x−5 (3 −5x)2=7 (3 −5x)2
h0(x) = 7
(3 −5x)2
c) Prouver que h0(x)>0 sur Dh; que peut-on en d´eduire pour les variations de h?
*Solution:
Sur Dh, (3 −5x)2>0 donc h0(x) est du signe de son num´erateur donc h0(x)>0

et donc hest strictement croissante sur Dh
h0(x)>0ethest strictement croissante sur Dh