Un certain regard sur le dénombrement et la loi binomiale

Vestiges d'une terminale S – Un certain regard sur le dénombrement et la loi binomiale - Un doc de Jérôme ONILLON distribué par la taverne de l'Irlandais Page 1 sur 4
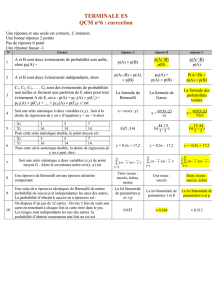
Quelques définitions
Définition de la factorielle d'un entier naturel
La factorielle d'un entier naturel non nul n est l'entier naturel noté
n!
et défini par :
Produit des n premiers entiers naturels
non nuls
n! 1 2 n= × × ×
…
Par exemple :
Produit des 5 premiers entiers
5! 1 2 3 4 5 120
= × × × × =
 . Par convention, on décrète :
0! 1
=
.
Définition d'un arrangement et d'une combinaison
E est un ensemble fini de cardinal n c'est-à-dire qu'il contient n éléments distincts.
p est un entier naturel tel que
p n
≤
.
 Un p-arrangement de E est une collection ordonnée de p éléments distincts de E..
Un arrangement de longueur n est appelé permutation de l'ensemble E.
 Une p-combinaison de E est une collection non ordonnée de p éléments distincts de E..
Autrement dit, une p-combinaison de E est un sous-ensemble de p éléments de E.
Pratiquement, un arrangement est le résultat d'un tirage successif et sans remise. Le
résultat du tiercé est un 3-arrangement de l'ensemble des chevaux participants. L'ordre
d'arrivée compte.
Une combinaison est le résultat d'un tirage par poignée ou simultané, où l'ordre n'a aucune
importance. Au loto, les six numéros tirés forment une 6-combinaison des 49 de départ.
La question qui nous intéresse est la suivante :
Combien un ensemble fini E de cardinal n possède-t-il de p-combinaisons c'est-à-dire de
sous-ensembles de p éléments ?
Le nombre de sous-ensembles : un cas particulier
Pour avoir une idée de ce qui se passe, voyons ce qu'il en est avec un cas particulier assez
simple. Cherchons combien l'ensemble
{
}
; ; ; ; ; ;
=
a b c d e f g
E admet de 3-combinaisons
c'est-à-dire de sous-ensembles de 3 éléments.
Pour répondre à cette interrogation, nous allons procéder par étapes.
 Combien existe-t-il de 3-arrangements possibles avec les sept lettres de E
EE
E ?
Un 3-arrangement est le résultat d'un tirage successif et sans remise où l'ordre a son
importance. Précisons que le 3-arrangement aef est différent du 3-arrangement eaf.
Versons les sept lettres de E dans une urne et procédons au tirage !
Première lettre Seconde lettre Troisième lettre
7 choix possibles 6 choix possibles car
une a déjà été tirée
5 choix possibles car
deux ont déjà été tirées
Conclusion : il y a donc
7 6 5 210
× × =
3-arrangements possibles.
Remarquons que :
1 2 3 4 5 6 7 7!
5 6 7
1 2 3 4 4!
× × × × × ×
× × = =
× × ×
 Combien E
EE
E contient-il de sous-ensembles de trois éléments ou de 3-combinaisons ?
La différence fondamentale entre un arrangement et une combinaison est l'ordre.
Les 3-combinaisons aef et eaf sont la même 3-combinaison.
Justement ! Avec la 3-combinaison aef, combien peut-on former de 3-arrangements ?
De combien de façons peut-on ranger ces trois lettres ? Simulons !
Première lettre Seconde lettre Troisième lettre
3 choix possibles 2 choix possibles car
une a déjà été utilisée
1 choix possible car
deux ont déjà été prises
Donc à partir de la 3-combinaison aef, on peut constituer
3 2 1 3! 6
× × = =
3-arrangements.
Et cette équivalence est valable pour toutes les 3-combinaisons ! Ainsi :
une 3-combinaison six 3-arrangements
=
Conclusion : il existe 210 7!
35
6 3! 4!
= =
× 3-combinaisons possibles. E contient 35 sous-
ensembles différents de trois éléments.
Le nombre de sous-ensembles : le cas général
Maintenant que nous nous sommes rôdés sur un cas particulier, passons au cas général
d'un ensemble E comportant n éléments distincts que nous appellerons lettres par abus de
langage. On dit que le cardinal de E est égal à n. Ce que l'on note :
(
)
Card n
=
E.
Soit p un entier naturel inférieur ou égal à n.
 Combien peut-on constituer de p-arrangements avec n éléments de E
EE
E ?
Constituer un p-arrangement, c'est procéder à un tirage successivement et sans remise de p
éléments parmi les n que compte E. Simulons !
Première lettre Seconde lettre Troisième lettre p-ième lettre
n choix possibles
n 1
−
choix
possibles
n 2
−
choix
possibles
n p 1
− +
choix
possibles
Conclusion : avec les n lettres de l'ensemble E, nous pouvons constituer exactement
( ) ( )
(
)
(
)
( ) ( )
1 n p n p 1 n
n!
n n 1 n p 1
1 n p n p !
× × − × − + × ×
× − × × − + = =
× × − −
… …
……
p-arrangements. Ce nombre de p-arrangements est noté
p
n
A
mais n'est pas au programme.

Vestiges d'une terminale S – Un certain regard sur le dénombrement et la loi binomiale - Un doc de Jérôme ONILLON distribué par la taverne de l'Irlandais Page 2 sur 4
 Combien E
EE
E contient-il de sous-ensembles de p éléments ou de p-combinaisons ?
Avec une p-combinaison c'est-à-dire avec p lettres distinctes à sa disposition, combien
peut-on constituer de p-arrangements ?
Première lettre Seconde lettre Troisième lettre p-ième lettre
p choix possibles
p 1
−
choix
possibles
p 2
−
choix
possibles
1
choix possible
Donc chaque p-combinaison correspond à
(
)
(
)
p p 1 p 2 1 p!
× − × − × × =
…
p-arrangments.
Conclusion : il existe
( )
Nombre de p-arrangements n!
p! n p ! p!
=
− ×
p-combinaisons.
Nombre de combinaisons : le "p parmi n"
Définition d'un "p parmi n" ou d'un coefficient binomial
n est un entier naturel non nul et p un autre entier naturel tel que
p n
≤
.
Le nombre noté
n
p
et se prononçant "p parmi n" est l'entier naturel défini par :
( ) ( ) ( )
p facteurs
Cette définition n'est valable que si p 0
n n 1 n p 1
nn!
pn p ! p! p!
≠
× − × × − +
  = =
  − ×
…
Tout ensemble de cardinal n contient
n
p
ou p-combinaisons
sous-ensembles ayant exactement p élémen
ts
.
Notation :
n
p
est la notation internationale du
p
n
C
français. Celui-ci se prononce "CNP".
Calculons quelques "p parmi n" particuliers. Dans ce qui suit, E est un ensemble de
cardinal n c'est-à-dire que E contient n éléments.
( )
n possède un seul sous-ensemble qui n'a
n! n! 1
0 aucun élément : l'ensemble vide noté .
n 0 ! 0! n! 1
= = = ⇔ 
∅
− × ×
E :
n contient n sous-ensembles
n n n
1 qui ont un seul élément !
1! 1
= = = ⇔ 
E :
( )
n n'a qu'un seul sous-ensemble
n! n! n! 1
n à n éléments : lui-même.
n n ! n! 0! n! 1 n!
= = = = ⇔ 
  − × × ×
E
 Avec les 49 boules du loto, il existe 49 49!
13983816
643! 6!
  = =
  ×
  tirages possibles.
La formule donnant le nombre de p-combinaisons est connue depuis le XIIème siècle.
Mais les deux propriétés qui viennent ne furent établies qu'au XVIème par Blaise Pascal.
Théorème : le nombre de combinaisons est symétrique
Si n et p sont deux entiers naturels tels que
p n
≤
alors
p n p
n n
n n C C
p n p
−
= ⇔ =
−
Comme 7 7
3 7 3 4
=
− =
alors dans un ensemble de sept éléments, il existe autant de
sous-ensembles de trois éléments que de sous-ensembles de quatre. A savoir 210.
Le théorème précédent peut être établi de deux manières :
Une première preuve de ce théorème : par les sous-ensembles
E est un ensemble de cardinal n.
Prendre p éléments de E d'un côté, c'est en laisser
n p
−
de l'autre.
La réunion des deux est l'ensemble
p élément
n p éléments
s−
FG
E
Dans l'ensemble E, tout sous-ensemble F de p éléments est associé à un sous-ensemble G
de
n p
−
éléments. G est le complémentaire de F dans E. Et réciproquement !
Dans E, il existe donc autant de sous-ensembles à p éléments que de sous-ensembles à
n p
−
éléments. Par conséquent :
n n
p n p
=
−
Une seconde preuve de ce théorème : par le calcul
Comme
(
)
n n p n n p p
− − = − + =
alors nous pouvons écrire :
( ) ( ) ( )
( )
( )
( )
( )
n n
n! n! n!
p n p
n p ! p! n p ! n n p ! n n p ! n p !
= = = =
−
− × − × − − − − × −
Théorème : la formule de Pascal
Si n et p sont deux entiers naturels tels que
p n
<
alors
n 1 n 1 n
p 1 p p
− −
+ =
−
.
Comme celui qui le précède, ce théorème peut être démontré de deux manières :

Vestiges d'une terminale S – Un certain regard sur le dénombrement et la loi binomiale - Un doc de Jérôme ONILLON distribué par la taverne de l'Irlandais Page 3 sur 4
Une première preuve de ce théorème : par les sous-ensembles
Soit E un ensemble de cardinal n et a un élément particulier de E.
Les
n
p
sous-ensembles de E contenant p éléments se répartissent en deux catégories :
Ceux qui contiennent a. Ceux qui ne contiennent pas a
{ }
A choisir
parmi les n 1 éléments de \
p éléments au total
p 1 éléments autres que
−
−
a
a a
E
{ }
A choisir
parmi les n 1 éléments de \
p éléments autres que
−
a
a
E
Au total, il en existe donc
n 1
p 1
−
−
Au total, il en existe
n 1
p
−
Conclusion :
n n 1 n 1
p p 1 p
− −
= +
−
Une seconde preuve de ce théorème : par le calcul
Pour établir l'égalité recherchée, partons du second membre !
( ) ( ) ( )
(
)
(
)
( ) ( ) ( ) ( )
(
)
( ) ( )
n 1 p 1 1 n 1 p 1
On met ces deux fractions au même dénominateur p!
Pour note : p! 1 2 p 1 p p 1 ! p
n 1 n 2 n p 1 n 1 n 2 n p
n 1 n 1
p 1 p p 1 ! p!
− − − + − − +
= × × × − × = − ×
− × − × × − + − × − × × −
− −
+ = +
−−
…
… …
( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( ) ( )
Facteurs... ...communs
n
p n 1 n p 1 n 1 n p 1 n p
p!
n 1 n p 1 p n p n n 1 n p 1
n
p
p! p!
× − × × − + + − × × − + × −
=
− × × − + × + − × − × × − +
= = =
… …
……
p=0 p=1 p=2 p=3 p=4
n=0 1
n=1 1 1
n=2 1
1 1 2
+ =
1
3 3 4
car
2 3 3
+ =
n=3 1
1 2 3
+ =
1 2 3
+ =
1
La formule de
Pascal permet de
calculer les "p
parmi n" en
cascades : c'est le
triangle de Pascal
En n'oubliant pas :
n n
1
0 n
= =
n=4 1
1 3 4
+ =
3 3 6
+ =
3 1 4
+ =
1
La formule du binôme
Théorème : la formule du binôme
Pour tous nombres complexes a et b et, pour tout entier naturel non nul n, on a :
( )
n
n n 1 k n k n 1 n
1 n n 1
n n n n n
a b .a .a .b .a .b .a.b .b
0 1 k n 1 n
− − −
= = =
+ = + + + + + +
−
… …
Cette formule permet de développer n'importe quelle puissance d'une somme. Ainsi :
( )
4
4 3 2 2 3 4 4 3 2 2 3 4
4 4 4
a b a .a .b .a .b .a.b b a 4.a .b 6.a .b 4.a.b b
1 2 3
+ = + + + + = + + + +
Note : c'est à cause de cette formule que les
n
p
sont appelés coefficients binomiaux.
La preuve de cette formule...par récurrence 
Nous allons établir cette formule du binôme par récurrence sur l'entier naturel no nul n.
 La formule est-elle vraie au premier rang pour
n 1
=
? Nous avons :
( )
1
1
1 0 0 1 n k k
k 0
Donc la formule est vraie au premier rang n 1.
1 1 1
a b a b 1 a 1 b .a .b .a .b .a .b
0 1 k
−
=
=
+ = + = × + × = + =
∑
 Supposons la formule vraie au rang n c'est-à-dire que :
( )
n
n
n k k
k 0
n
a b .a .b
k
−
=
+ =  
∑.
Montrons qu'alors elle est aussi vraie au rang
n 1
+
.
( ) ( ) ( )
( )
n 1 n
n n n
n k k n 1 k k n k k 1
k 0 k 0 k 0
On a distribué a On a distribué b
D'après l'hypothèse
de récurrence.
a b a b a b
n n n
a b .a .b .a .b .a .b
k k k
+
− + − − +
= = =
+ = + × +
= + × = +
∑ ∑ ∑
n+1
n n 1
n 1 n 1 k k n k k 1 n 1
k 1 k 0
Au lieu de commencer la somme à k 0, Au lieu de terminer la somme à k n,
on débute la somme à k 1 et on sort a . on a
n n
a .a .b .a .b b
k k
−
+ + − − + +
= =
==
=
= + + +
∑ ∑
n+1
chève la somme à k n 1 et on sort b .
n n
n 1 n 1 k k n 1 i i n 1
k 1 i 1
On ré-indexe en posant i k 1 ou k i 1.
n n
a .a .b .a .b b
k i 1
= −
+ + − + − +
= =
= + = −
= + + +
−
∑ ∑

Vestiges d'une terminale S – Un certain regard sur le dénombrement et la loi binomiale - Un doc de Jérôme ONILLON distribué par la taverne de l'Irlandais Page 4 sur 4
( )
n 1 j j
n
n 1 n 1 n 1 j j n 1 j j n 1
j 1
j k i : peu importe l'indice...
n
n 1 n 1 j j
j 1
On a factorisé par a .b
n n
a b a .a .b .a .b b
j j 1
n n
a .a .b
j j 1
+ −
++ + − + − +
=
= =
+ + −
=
+ = + + +
−
= + +
−
∑
∑
n 1
.
Et on peut appliquer la formule de Pascal
n n 1
n 1 n 1 j j n 1 n 1 j j
j 1 j 0
1 1
b
n 1 n 1 n 1 n 1
.a .a .b .b .a .b
0 j n 1 j
+
+
+ + − + + −
= =
= =
+
+ + + +
= + + =
+
∑ ∑
Donc la formule est alors vraie au rang
n 1
+
. D'où le théorème.
 Le nombre total de sous-ensembles d'un ensemble E
EE
E de cardinal n
Si E est un ensemble de cardinal n, alors tous ses sous-ensembles ont entre 0 et n éléments.
Le nombre de sous-ensembles de E ayant exactement p éléments est donné par
n
p
.
D'après la formule du binôme, nous pouvons écrire :
( )
n
n
n n k n
1
k 0
Somme de tous les sous-ensembles de
n n n n n n
2 1 1 1 1
k 0 1 p n 1 n
−
=
=
= + = × × = + + + + + +
−
∑… …
E
Conclusion : un ensemble E de cardinal n possède exactement
n
2
sous-ensembles.
Schéma de Bernoulli et loi binomiale
Définition d'une expérience ou épreuve de Bernoulli
Une expérience ou épreuve de Bernoulli est une expérience aléatoire qui n'a que deux
issues possibles. On appelle souvent celles-ci Succès et Echec.
Une épreuve de Bernoulli peut être représentée par l'arbre
ci-contre.
Si on appelle p la probabilité d'obtenir un succès S alors la
probabilité d'obtenir un échec E est égal à 1
= −
q p
.
E étant l'événement contraire de S, il est également noté
S
.
L'exemple classique d'une expérience de Bernoulli est le jeu de pile ou face. Si la pièce est
bien équilibrée, les probabilités p et q des événements S et E sont égales à
0,5
.
Définition d'un schéma de Bernoulli et d'une loi binomiale
Un schéma de Bernoulli est une expérience aléatoire qui consiste à répéter un certain
nombre de fois et de manière indépendante une même épreuve de Bernoulli.
Si on appelle X la variable aléatoire qui comptabilise le nombre de succès S obtenus à un
schéma de Bernoulli de n épreuves, alors la loi de probabilité de X est appelée loi
binomiale de paramètres n et p et, est notée
(
)
B n,
p
.
 Déterminons la loi de probabilité de X
La variable X étant égale au nombre de succès obtenus au cours des n épreuves, elle prend
toutes les valeurs entières comprises entre 0 et n.
Pour tout entier
{
}
k 0;1; ;n
∈
…
, déterminons
(
)
p X k
=
.
Autrement dit, quelle est la probabilité qu'au cours des n épreuves du schéma, on obtienne
exactement k succès S et donc
n k
−
échecs E ?
On peut voir le résultat d'un schéma de Bernoulli de n épreuves comme étant un mot de n
lettres composé avec les seuls caractères S et E.
Epreuve 1 Epreuve 2 Epreuve 3 Epreuve n
S ou E S ou E S ou E S ou E
Les mots qui nous intéressent sont ceux comportant k caractères S et
n k
−
caractères E.
La probabilité d'obtenir un seul de ces mots est donnée par k n k
Chaque S a pour probabilité .
Chaque E a pour probabilité .
−
×
p
q
p q
 .
Mais combien peut-on constituer de mots comportant exactement k S et
n k
−
E ?
Chacun de ces mots est caractérisé par les places occupées par les S.
Pour chacun de ces mots, l'ensemble F des numéros des places occupées par les S est un
sous-ensemble de k éléments de l'ensemble de toutes les places possibles
{
}
1;2; ;n
=
…
E.
Il y a autant de sous-ensembles F de k éléments dans E qu'il y a de mots ayant
exactement k caractères S et
n k
−
caractères E. Donc il existe
n
p
mots possibles.
Théorème : loi de probabilité d'une loi binomiale
Si X est la variable aléatoire associée à la loi binomiale
(
)
B n,
p
alors
Pour tout
{
}
k 0;1; ;n
∈
…
,
( ) ( )
n k
k
n
p X k 1
k
−
= = × × −
  p p
Enfin leurs démonstrations étant apocalyptiques, on admettra que :
 L'espérance de la loi binomiale
(
)
B n,
p
est donnée par :
(
)
E X n p
= ×
.
 La variance de la loi binomiale
(
)
B n,
p
est donnée par :
(
)
(
)
V X n 1
= × × −
p p
.
S Succès
=
S ou E Echec
=
p
1
= −
q p
p
Epreuve de Bernoulli