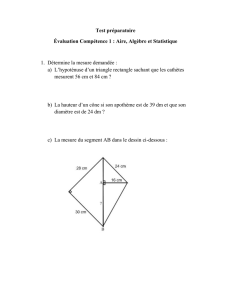
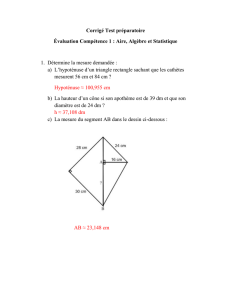
1 Produits tensoriels. - IMJ-PRG

Universit´e de Paris VI Master M1 2009-2010
D. Bertrand Alg`ebre g´eom´etrique
CHAPITRE IV
G´ EOM´ ETRIE MULTILIN´ EAIRE
1 Produits tensoriels.
Dans ce paragraphe, on consid`ere des espaces vectoriels, de dimension ´eventu-
ellement infinie, sur un corps (commutatif) Kquelconque. En premi`ere
lecture, on pourra les supposer tous de dimension finie.
1.1 D´efinition
Soient Vet Wdeux espaces vectoriels. On cherche `a construire un espace
vectoriel V⊗Wtel que la donn´ee d’une forme bilin´eaire bsur V×W´equivale
`a celle d’une forme lin´eaire fbsur V⊗W. Plus g´en´eralement, on ´etudie le
“probl`eme universel” suivant.
Existe-t-il un couple (E, β)form´e d’un espace vectoriel Eet d’une appli-
cation bilin´eaire β:V×W→Ev´erifiant la propri´et´e suivante : pour toute
application bilin´eaire bde V×Wvers un espace vectoriel Uquelconque, il
existe une unique application lin´eaire f=fb:E→Utelle que
pour tout (v, w)∈V×W, b(v, w) = fbβ(v, w),
autrement dit, telle que b=fb◦β.
Du fait de la condition d’unicit´e, deux solutions (E, β),(E0, β0) de ce
probl`eme sont li´ees par un isomorphisme K-lin´eaire φ:E→E0tel que
φ◦β=β0. S’il y a une solution, elle est donc unique `a isomorphisme pr`es.
On va montrer qu’il existe une solution. On la d´esignera (`a isomorphisme
pr`es) par (E=V⊗W, β). Pour tout (v, w)∈V×W, on ´ecrira
β(v, w) := v⊗w∈V⊗W,
1

de sorte que la bilin´earit´e de βse traduit par les relations:
∀v, v0∈V, w, w0∈W, λ ∈K , (λv)⊗w=v⊗(λw) = λ(v⊗w);
v⊗(w+w0) = v⊗w+v⊗w0,(v+v0)⊗w=v⊗w+v0⊗w.
Lorsqu’on veut pr´eciser le corps des scalaires K, on ´ecrit V⊗KW. On
dit que V⊗KWest “le” produit tensoriel de Vpar Wsur K. Ses ´el´ements
s’appellent des tenseurs, ceux de la forme v⊗wdes tenseurs purs (ou
d´ecompos´es). Attention: une somme v⊗w+v0⊗w0∈V⊗Wn’est en
g´en´eral pas un tenseur pur !
Existence du produit tensoriel.
Premi`ere preuve : soit El’espace vectoriel form´e par toutes les applications
ensemblistes de V×Wdans Knulles en dehors d’un sous-ensemble fini de
V×W. Il admet pour base {δ(v,w),(v, w)∈V×W}o`u δxd´esigne la fonction
de Dirac relative au point x∈V×W. Consid´erons le sous-espace vecto-
riel Fde Eengendr´e par les ´el´ements δ(v,w+w0)−δ(v,w)−δ(v,w0), δ(v+v0,w)−
δ(v,w)−δ(v0,w), δ(λv,w)−λδ(v,w), δ(v,λw)−λδ(v,w), ainsi que l’espace vectoriel
quotient E=E/F. Alors, β:V×W→E:β(v, w) := classe de δ(v,w)
dans E, est une application bilin´eaire de V×Wdans E, dont l’image
ensembliste β(V×W) engendre l’espace vectoriel E. Pour toute applica-
tion b:V×W→U, l’application ˜ fb:E → Uqui attache `a un ´el´ement
Σ(v,w)∈A⊂V×W,A fini λ(v,w)δ(v,w)de El’´el´ement Σ(v,w)∈Aλ(v,w)b(v, w) de Uest
bien d´efinie (car les δ(v,w)forment une base de E), et est lin´eaire. Si best de
plus bilin´eaire, ˜ fbs’annule sur F, et d´efinit donc par passage au quotient par
Fune application lin´eaire fb:E→U, qui v´erifie bien fb◦β=b. Enfin, fb
est la seule application lin´eaire de Edans Uv´erifiant cette propri´et´e, puisque
l’image de βengendre Etout entier.
Deuxi`eme preuve: soient {ei;i∈I},{j;j∈J}des bases de V, W .` A tout
(i, j)∈I×J, attachons un symbole mi,j et consid´erons l’espace vectoriel
E:= ⊕(i,j)∈I×JK.mi,j , de base {mi,j ,(i, j)∈I×J}. Il existe alors une
(unique) application bilin´eaire β:V×W→Etelle que β(ei, j) = mi,j
pour tout (i, j)∈I×J. Soit maintenant b:V×W→Uune application
bilin´eaire. Puisque les mi,j forment une base de E, il existe une unique
application lin´eaire fb:E→Utelle que f(mi,j ) = b(ei, j) pour tout (i, j)∈
I×J. De la bilin´earit´e de bet de β, et de la lin´earit´e de fb, on d´eduit
alors que pour tout v= Σi∈Afini ⊂Iλiei∈V , w = Σj∈Bfini ⊂Jµjj∈W, on
a: b(v, w)=Σ(i,j)∈A×Bλiµjb(ei, j) = fb(Σ(i,j)∈A×Bλiµjmi,j ) = fb(β(v, w)).
Ainsi, l’application lin´eaire fbv´erifie la propri´et´e requise, et c’est la seule
2

puisque que l’image de βcontient la base mi,j de E. On voit ainsi de plus
que
Th´eoreme 1.1. : si V,Wsont des espaces vectoriels de dimension finies
n, m, de bases {ei,1≤i≤n},{j,1≤j≤m}, alors V⊗West un espace
vectoriel de dimension nm, de base {ei⊗j,1≤i≤n, 1≤j≤m}.
Remarques:
i) pour V=K, l’application bilin´eaire K×W→W: (λ, w)7→ λw
´etablit un isomorphisme canonique K⊗W'W.
ii) Inversion: L’application bilin´eaire V×W→W⊗V: (v, w)→w⊗v
´etablit un isomorphisme canonique V⊗W'W⊗V. Mais attention quand
V=W: dans V⊗V,v⊗v0n’est ´egal `a v0⊗vque si vet v0sont colin´eaires.
iii) Complexification : soit Vun espace vectoriel sur R, de dimension n.
Comme Cest un ev de dimension 2 sur R, on peut former C⊗RV:= VC,
qui est un R- ev de dimension 2n. De plus, pour tout λ∈C, l’application
C×V→VC: (µ, v)7→ λµ⊗vest R-bilin´eaire, donc induit un endomorphisme
R-lin´eaire mλde VC. On v´erifie que mλ+mλ0=mλ+λ0, mλ◦mλ0=mλλ0, m1=
idVC, de sorte que la loi C×VC3(λ, v)7→ λ.v:= mλ(v)∈VCmunit VCd’une
structure d’espace vectoriel sur C, de dimension nsur C. Un tel C-ev est
naturellement muni d’un involution C-antilin´eaire σ=c:VC→VC, appel´ee
conjugaison complexe, et d´efinie `a partir des relations c(λ⊗v) = λ⊗v.
On r´ecup`ere la structure r´eelle en notant que {v∈VC, c(v) = v}co¨ıncide
avec 1 ⊗V, qu’on identifie `a V. Ceci montre d’ailleurs qu’il n’y a pas de
conjugaison complexe naturelle sur un C-espace vectoriel g´en´eral (les essais
“´evidents” d´ependent du choix d’une base).
iv) K-alg`ebres : ce sont les K-espaces vectoriels Amunis d’une application
lin´eaire µ:A⊗A→A. Traduire ce que cela signifie en terme de la loi de
composition interne (a, b)7→ a.b := µ(a⊗b). Pour l’associativit´e, qui n’est
pas requise dans la d´efinition d’une K-alg`ebre (penser aux alg`ebres de Lie),
voir le §2.1 ci-dessous.
v) Soient V1⊂V, W1⊂Wdeux sous-espaces vectoriels. Alors, l’applica-
tion V1×W13(v1, w1)7→ v1⊗w1∈V⊗Wfournit une application lin´eaire
injective ι:V1⊗W1→V⊗W, qui permet d’identifier V1⊗W1`a un sous-
espace vectoriel de V⊗W.
vi) (Hors programme) Attention toutefois : si une bonne partie des
´enonc´es de ce chapitre s’´etend sans difficult´e au cas des modules sur un an-
neau commutatif, ce n’est pas le cas pour l’injectivit´e de ιau (v) pr´ec´edent.
3

Ainsi, le Z-module V=Zadmet V1= 2Z'Zcomme sous-module, et
en consid´erant le Z-module W=Z/2Z, on a V1⊗ZW'Z⊗ZW'W,
tandis que le produit tensoriel dans V⊗ZWd’un ´el´ement 2n∈V1par
1∈Wvaut (2n)⊗Z1 = 2(n⊗Z1) = n⊗Z2.1 = n⊗Z0 = 0. L’application
ι:V1⊗ZW→V⊗ZWest donc ici identiquement nulle.
1.2 Propri´et´es fonctorielles
Th´eoreme 1.2. Soient g:V→V0, h :W→W0deux applications lin´eaires.
Alors, il existe une unique application lin´eaire, not´ee
g⊗h:V⊗W→V0⊗W0
telle que pour tout (v, w)∈V×W, on ait (g⊗h)(v⊗w) = g(v)⊗h(w).
Preuve : l’application b:V×W→V0⊗W0: (v, w)7→ g(v)⊗h(w) est
bilin´eaire. L’application lin´eaire correspondante fbest donc la seule v´erifiant
ces conditions, et on la note fb:= g⊗h.
Mais cette notation impose de v´erifier une compatibilit´e. Les applications
g, h appartiennent aux espaces vectoriels L(V, V 0),L(W, W 0), et la notation
g⊗hrepr´esente d´ej`a un ´el´ement de leur produit tensoriel. Heureusement,
l’application L(V, V 0)× L(W, W 0)→ L(V⊗W, V 0⊗W0):(g, h)7→ fbfournit
une application lin´eaire canonique
κ:L(V, V 0)⊗ L(W, W 0)→ L(V⊗W, V 0⊗W0),
envoyant bien g⊗h(au sens du membre de gauche) sur fb. Elle est injective,
mais pas surjective en g´en´eral (voir le th´eor`eme 2).
Transcription matricielle : supposons V0=V, W 0=Wde dimensions finies
n, m, et soient A, B les matrices repr´esentatives (n×n),(m×m) de g, h dans
des bases ei, jde V, W . Alors, la matrice repr´esentative de l’endomorphisme
g⊗hde V⊗Wdans la base ei⊗jest donn´ee par le produit de Kronecker
A⊗Bde Apar B: c’est la matrice (nm ×nm) obtenue en remplacant
chaque coefficient ai,i0de Apar le bloc ai,i0B.
Pour tout espace vectoriel V, notons V∗:= L(V, K) le dual de V. Si V
est de dimension finie, et muni d’une base {e1, ..., en}, on notera {e∗
1, ..., e∗ n}
la base duale de V∗, d´efinie par e∗
j(ei) = δi,j ,1≤i, j ≤n. On rappelle que le
rang d’une application lineaire est la dimension de son image.
4

Th´eoreme 1.3. : soient V, W deux espaces vectoriels.
i) Il existe une unique injection lin´eaire
φ:V∗⊗W → L(V, W ),
telle que pour tout ∈V∗, w ∈W, v ∈V, on ait φ(⊗w)(v) = (v)w.
ii) L’image de φest form´ee des applications lin´eaires de Vdans Wde rang
fini. En particulier, si Vou West de dimension finie, φest un isomorphisme.
iii) Si W=Vest de dimension finie, et si u∈End(V)est l’image par
φde Σαα⊗vα, alors sa trace vaut T r(u)=Σαα(vα). Dans les bases
d´ecrites plus haut, l’application identit´e u=idVde Vest l’image par φde
Σi=1,...ne∗
i⊗ei.
Preuve : i) pour d´efinir φ(qui est un cas particulier de l’application κsupra),
consid´erer l’application bilin´eaire V∗×W→ L(V, W ) : (, w)7→ {v7→
(v)w}. Pour l’injectivit´e, choisissons des bases {i, i ∈I},{j, j ∈J}de
V∗, W . Alors, les {i⊗j,(i, j)}forment une base de V∗⊗W, et il suf-
fit de montrer que leurs images par φsont des applications de Vdans W
lin´eairement ind´ependantes. Dans le cas contraire, celles-ci enverraient tout
vecteur vde Esur des vecteurs i(v)jde Wli´es. Les j´etant lin´eairement
ind´ependants, on aurait donc i(v) = 0 pour tout i∈I, v ∈V, et les i
seraient toutes nulles.
ii) Comme V∗⊗West form´e de combinaisons lin´eaires finies des i⊗j,
leurs images par φsont bien de rang fini. Invers´ement, soit u:V→W,
d’image W0de dimension finie, et soit {1, .., m}une base de W0. Le lecteur
concluera en la compl´etant en une base {j, j ∈J}de W. Enfin, si Vou W
est de dimension finie, tout uest de rang fini.
iii) En compl´etant un ´el´ement non nul , resp. w, de V∗, resp. Wen une
base de V∗, W , et en consid´erant la base duale correspondante dans V, on
voit que φ(⊗w) est repr´esent´ee par une matrice Udont le seul coefficient
non nul est U1,1=(w). Sa trace vaut donc (w), et la lin´earit´e de φet
de T r permet de conclure. Voici une fa¸con plus intrins`eque de pr´esenter
les choses : la forme bilin´eaire V∗×V→K: (, v)7→ (v) d´efinit une
forme lin´eaire canonique (appel´ee: contraction) T:V∗⊗V→K. Alors,
T◦φ−1est une forme lin´eaire sur End(V), qui coincide avec T r sur les
endomorphismes de type φ(⊗v). Pour la deni`ere assertion, noter que pour
tout k,φ(Σie∗
i⊗ei)(ek) = Σiδi,kei=ek=idV(ek). On retrouve ainsi la
formule T r(idV) = T(Σie∗
i⊗ei) = Σie∗ i(ei) = n=dimV (´evidente, mais qui
peut servir de d´efinition de la dimension de V).
5