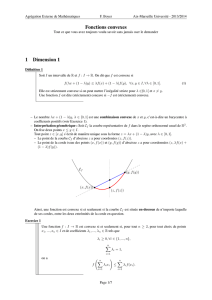
Définitions mathématiques importantes

f∶X→RC∈X
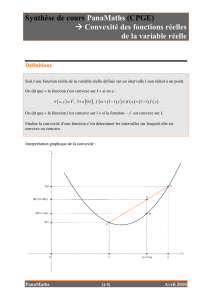
∀(x, y)∈C2,∀t∈]0,1[
f(tx +(1−t)y)<tf(x)+(1−t)f(y)
f∶X→R−f
f∶X→RC∈X∀(x, y)∈
C2,∀t∈[0,1]
f(tx +(1−t)y)≥min(f(x), f(y))

f∶X→RC∈X
∀(x, y)∈C2,∀t∈]0,1[
f(tx +(1−t)y)>min(f(x), f(y))
●
●f g
g○f

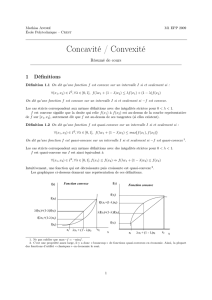
SRn∀(x, y)∈S2,∀λ∈[0,1]
(1−λ)x+λy ∈S
SRn∀(x, y)∈S2,∀λ∈]0,1[
(1−λ)x+λy ∈S
E d ∶E×E→R+E(E, d)
∀x0∈E∀r>0
r
B(x, r)={x∈E, d(x, x0)<r}

r
B(x, r)={x∈E, d(x, x0)≤r}
R C d(x, y)=x−y
S E E ∀x∈S >0
B(x, )∈S
S′E E S′
E E
S(E, d)S M ∈R
∀(x, y)∈S d(x, y)≤M
f(x, y)
x
∂f (x, y)
∂x
f(x, y)df
df=∂f (x, y)
∂x dx+∂f(x, y)
∂y dy
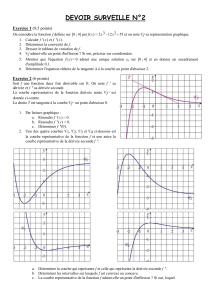
 6
6
 7
7
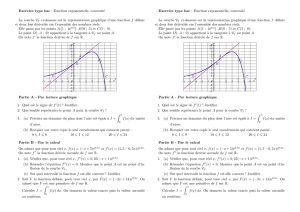
1
/
7
100%