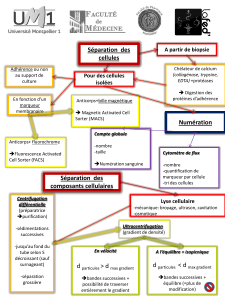
TD n˚2 : Fonctions à plusieurs variables

TD n˚2 : Fonctions à plusieurs variables
Exercice 1
Préciser si les domaines D⊂R2suivants sont fermés ou non, ouverts ou non, bornés ou non.
1. D=R2.
2. D=R+×R+.
3. D=R+×R+
∗.
4. D={(x, y)|x≥0, y ≥0, x +y≤1}.
5. D={(x, y)|x2+y2<5}.
6. D={(x, y)|2x+ 3y≤1}.
Exercice 2
Déterminer la régularité des fonctions suivantes sur leur domaine et calculer leur gradient là où c’est
possible.
1. f(x, y) = xy sur D=R2.
2. f(x, y) = cos(x) sin(y)sur D=R2.
3. f(x, y) = x3+ 2y2sur D=R2.
4. f(x, y) = xy
x2+y2si (x, y)6= (0,0),
0si (x, y) = (0,0),sur D=R2.
5. f(x, y) = px2+y2sur D=R2.
Exercice 3 : Un peu d’économie !
Definition. Si f:D⊂R2→Rest une fonction de deux variables ne s’annulant pas et admettant des
dérivées partielles en un point (x0, y0)de D, on définit son élasticité partielle par rapport à la première
variable en (x0, y0)comme suit :
εxf(x0, y0) = lim
h→0
f(x0+h)−f(x0)
f(x0)
h
x0
=x0
f(x0)
∂f
∂x (x0, y0)
1. Déterminer les élasticités partielles par rapport aux variables xet yde la fonction de Cobb-Douglas
suivante : f(x, y) = kxαyβ, où k,αet βsont des constantes réelles positives, et observer qu’elles
ne dépendent pas du point (x0, y0)choisi dans ]0,+∞[×]0,+∞[.
2. Etendre le résultat à une fonction de Cobb-Douglas à nvariables : f(x1, . . . , xn) = kxα1
1· · · xαn
n.
3. Tracer dans (R+?)2l’allure des lignes de niveau de la fonction u(x, y) = xy2. Ce sont les courbes
d’indifférence pour la fonction utilité u.
1

Exercice 4 : Courbes de niveau
Tracer dans R2l’allure des courbes de niveau des fonctions suivantes, par exemple pour les valeurs
entières :
1. f(x, y) = xy.
2. f(x, y) = 1
x2+y2.
3. f(x, y) = x2−y2.
4. f(x, y) = x2−y.
5. f(x, y) = y2−x2+x3. Dans ce dernier cas, on pourra s’aider de la calculatrice et constater la
cohérence du résultat avec la direction et norme du gradient en quelques points.
Exercice 5 : Pont aux ânes
Soit f:R2→Rune fonction de deux variables admettant des dérivées partielles en tout point. Dériver
les fonctions u(x) = f(x, −x)et g(x, y) = f(y, x).
Exercice 6 : Théorème de Schwarz
1. Vérifier l’énoncé du théorème de Schwarz pour les fonctions C2suivantes :
f(x, y) = xexp(xy), f (x, y) = ln(x2+y2+ 1), f(x, y)=(y+ 2) tan(x).
2. Prouver que fdéfinie de la manière suivante n’est pas de classe C2en 0:
f(x, y) = (xy3
x2+y2si (x, y)6= (0,0),
0si (x, y) = (0,0).
Exercice 7
Soit F:R→Rune fonction de classe C1. Montrer que la fonction fdéfinie de la manière suivante est
continue sur R2:
f(x, y) = (F(x)−F(y)
x−ysi x6=y,
F0(x)si x=y.
Exercice 8 : Retour sur la convexité
Soit f:I→Rune fonction, où Iest un intervalle de R. Montrer que fest convexe si et seulement si
l’ensemble {(x, y)∈I×R|y≥f(x)}, appelé épigraphe de f, est convexe.
Exercice 9 : Fonction coercive
1. Soit f:Rd→Rune fonction continue et coercive : pour toute suite (un)n∈Nà valeurs dans Rd
telle que kunk → +∞lorsque n→+∞,f(un)→+∞(on note aussi limkxk→+∞f(x) = +∞).
Montrer que fadmet un minimum global.
2. Si fest une fonction de classe C1de Rddans Rtelle que limkxk2→+∞f(x)
kxk2= +∞, montrer que
l’application gradient ∇f:Rd→Rdest surjective, c’est-à-dire que pour tout `dans Rd, il existe
un point xde Rdtel que ∇f(x) = `.
Indice : on utilisera le fait que pour tout `dans Rd, le gradient de la fonction linéaire x7→ `·x
définie de Rddans Rest constant, égal à `.
2